Question

如图，在平面直角坐标系中，已知A、B、C三点

        的坐标分别为A（－2，0），B（6，0），C（0，3）.

  (1)求经过A、B、C三点的抛物线的解析式；

  (2)过Ｃ点作CD平行于轴交抛物线于点D，写出D点的坐标，

     并求AD、BC的交点E的坐标；

  (3)若抛物线的顶点为Ｐ，连结ＰC、ＰD，判断四边形CEDP的形状，

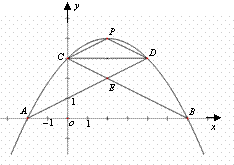     并说明理由.

Answer 1

解：⑴  由于抛物线经过点，

      可设抛物线的解析式为，则，　　　　　　　　　

      解得

    ∴抛物线的解析式为   ……………………4分

⑵  的坐标为       ……………………………5分

直线的解析式为

直线的解析式为    由

　  求得交点的坐标为　 ……………………………8分

⑶　连结交于，的坐标为

又∵，

　　∴，且

　    　∴四边形是菱形