题目内容
17．将二次函数y=x2的图象向左平移3个单位后，再向下平移5个单位，所得函数图象的解析式是y=（x+3）2-5．分析 抛物线平移不改变a的值，根据已知条件得到平移前后抛物线顶点坐标，然后由抛物线的顶点坐标写出平移后抛物线的解析式．
解答 解：原抛物线的顶点为（0，0），向左平移3个单位，再向下平移5个单位，那么新抛物线的顶点为（-3，-5），
可设新抛物线的解析式为：y=（x-h）2+k，代入得：y=（x+3）2-5．
故答案是：y=（x+3）2-5．
点评 主要考查了函数图象的平移，抛物线与坐标轴的交点坐标的求法，要求熟练掌握平移的规律：左加右减，上加下减．并用规律求函数解析式．
练习册系列答案
期末集结号系列答案
相关题目
9．
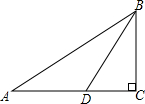如图，在Rt△ABC中，∠C=90°，BD是角平分线，若CD=m，AB=n，则△ABD的面积是（ ）
如图，在Rt△ABC中，∠C=90°，BD是角平分线，若CD=m，AB=n，则△ABD的面积是（ ）| A． | mn | B． | $\frac{1}{2}mn$ | C． | 2mn | D． | $\frac{1}{3}mn$ |
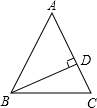如图，在△ABC中，AB=AC，BD⊥AC，D是垂足，DC=4，cosA=$\frac{3}{5}$，求tanC的值．