Question

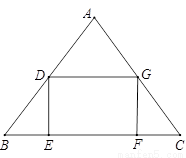
1．已知：如图，点E、F分别在?ABCD的边AB、CD的延长线上，且BE=DF．求证：AC、EF互相平分．

Answer 1

分析 根据平行四边形的性质可得出AB∥CD，AB=CD，∠A=∠C，再根据平行线的性质得出∠E=∠F，利用ASA即可得出结论．

解答 证明：在?ABCD中，AB∥CD，AB=CD，∠A=∠C，
∴∠E=∠F
∵BE=DH，
∴AE=CH，
在△AEG与△CHF中，
$\left\{\begin{array}{l}{∠BAD=∠BCD}\\{AE=CF}\\{∠E=∠F}\end{array}\right.$，
∴△AEG≌△CHF（ASA），
∴AE=CF，
∵AE∥CF，
∴四边形AECF是平行四边形，
∴AC、EF互相平分．

点评 本题考查了平行四边形的性质及全等三角形的判定；熟练掌握平行四边形的性质，证明三角形全等是解决问题的关键．