Question

16．从△ABC（CB＜CA）中裁出一个以AB为底边的等腰△ABD，并使得△ABD的面积尽可能大．
（1）用尺规作图作出△ABD．（保留作图痕迹，不要求写作法、证明）
（2）若AB=2m，∠CAB=30°，求出的△ABD的面积．

Answer 1

分析 （1）直接利用线段垂直平分线的性质作出AB的垂直平分线，交AC于点D，进而得出△ABD；
（2）利用锐角三角形关系得出DE的长，进而利用三角形面积求法得出答案．

解答 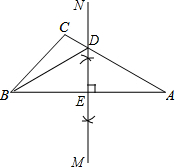解：（1）如图所示：△ABD即为所求；

（2）∵MN垂直平分AB，AB=2m，∠CAB=30°，
∴AE=1m，
则tan30°=$\frac{DE}{AE}$=$\frac{DE}{1}$，
解得：DE=$\frac{\sqrt{3}}{3}$．
故裁出的△ABD的面积为：$\frac{1}{2}$×2×$\frac{\sqrt{3}}{3}$=$\frac{\sqrt{3}}{3}$（m²）．

点评 此题主要考查了复杂作图以及线段垂直平分线的性质与作法、三角形面积求法、锐角三角函数关系等知识，熟练应用线段垂直平分线的性质是解题关键．