题目内容
19.解关于x的方程:$\frac{x+b}{x-a}$+$\frac{x+a}{x-b}$=2.分析 分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:去分母得:x2-b2+x2-a2=2x2-2(a+b)x+2ab,
移项合并得:2(a+b)x=(a+b)2,
当a+b=0时,x为不等于a、b的任意实数,
当a+b≠0时,x=a+b,
经检验是分式方程的解.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
9.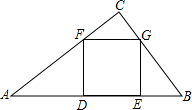 如图,在Rt△ABC中,∠C=90°,BC=6,AC=8,四边形DEGF为内接正方形,那么AD:DE:EB为( )
如图,在Rt△ABC中,∠C=90°,BC=6,AC=8,四边形DEGF为内接正方形,那么AD:DE:EB为( )
 如图,在Rt△ABC中,∠C=90°,BC=6,AC=8,四边形DEGF为内接正方形,那么AD:DE:EB为( )
如图,在Rt△ABC中,∠C=90°,BC=6,AC=8,四边形DEGF为内接正方形,那么AD:DE:EB为( )| A. | 16:12:9 | B. | 16:9:25 | C. | 9:12:16 | D. | 3:4:5 |
7.在△ABC中,AB=AC=5,sinB=$\frac{4}{5}$,那么△ABC的面积为( )
| A. | 10 | B. | 12 | C. | 14 | D. | 16 |
 已知:如图,在四边形ABCD中,AB=3,BC=12,CD=8,AD=4,BD=6,求证:BD平分∠ABC.
已知:如图,在四边形ABCD中,AB=3,BC=12,CD=8,AD=4,BD=6,求证:BD平分∠ABC.