题目内容
3.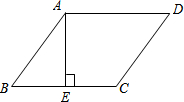 如图,在?ABCD中,AE⊥BC于E,AE=EB=EC=a,且a是一元二次方程x2-2x-3=0的根,则?ABCD的周长为( )
如图,在?ABCD中,AE⊥BC于E,AE=EB=EC=a,且a是一元二次方程x2-2x-3=0的根,则?ABCD的周长为( )| A. | 4+2$\sqrt{2}$ | B. | 12+6$\sqrt{2}$ | C. | 2+2$\sqrt{2}$ | D. | 4+2$\sqrt{2}$或12+6$\sqrt{2}$ |
分析 由a是一元二次方程x2-2x-3=0的根,即可求得a的值,又由AE=EB=EC=a,即可求得BC的长,由AE⊥BC,由勾股定理即可求得AB的长,然后由四边形ABCD是平行四边形,即可求得?ABCD的周长.
解答 解:∵x2-2x-3=0,
∴(x-3)(x+1)=0,
解得:x1=3,x2=-1,
∵AE=EB=EC=a,且a是一元二次方程x2-2x-3=0的根,
∴a=3,
∴AE=EB=EC=3,
∵AE⊥BC,
∴AB=$\sqrt{A{E}^{2}+E{B}^{2}}$=3$\sqrt{2}$,
∵四边形ABCD是平行四边形,
∴CD=AB=3$\sqrt{2}$,AD=BC=EB+EC=6,
∴?ABCD的周长为:AB+BC+CD+AD=12+6$\sqrt{2}$.
故选B.
点评 此题考查了平行四边形的性质、勾股定理以及一元二次方程的解法.注意平行四边形的对边相等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.某工艺厂计划一周生产工艺品2100个,平均每天生产300个,但实际每天生产量与计划相比有出入.下表是某周的生产情况 (超产记为正、减产记为负):
(1)写出该厂星期一生产工艺品的数量;
(2)本周产量中最多的一天比最少的一天多生产多少个工艺品?
(3)请求出该工艺厂在本周实际生产工艺品的数量.
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减(单位:个) | +5 | -2 | -5 | +15 | -10 | +16 | -9 |
(2)本周产量中最多的一天比最少的一天多生产多少个工艺品?
(3)请求出该工艺厂在本周实际生产工艺品的数量.
14.下列各组代数式中,属于同类项的是( )
| A. | 4ab和4abc | B. | $\frac{2}{3}$a2b和$\frac{2}{3}$ab2 | C. | -mn和mn$\frac{3}{2}$ | D. | x2y和x2 |
11.下列计算正确的是( )
| A. | b4•b4=2b4 | B. | (x3)3=x6 | C. | 70×8-2=$\frac{1}{64}$ | D. | (-bc)4÷(-bc)2=-b2c2 |
 如图所示的一块土地,经测量可知AD=12m,CD=9m,∠ADC=90°,AB=39m,BC=36m,根据测量得出的数据,则这块土地的面积为216m2.
如图所示的一块土地,经测量可知AD=12m,CD=9m,∠ADC=90°,AB=39m,BC=36m,根据测量得出的数据,则这块土地的面积为216m2. 暑假将至,某商场为了吸引顾客,设计了可以自由转动的转盘(如图所示,转盘被均匀地分为20份),并规定:顾客每 200元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得200元、100元、50元的购物券,凭购物券可以在该商场继续购物.若某顾客购物300元.
暑假将至,某商场为了吸引顾客,设计了可以自由转动的转盘(如图所示,转盘被均匀地分为20份),并规定:顾客每 200元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得200元、100元、50元的购物券,凭购物券可以在该商场继续购物.若某顾客购物300元.