题目内容
13．若多项式x2+mx+4能用完全平方公式分解因式，则m的值是±4．分析 利用完全平方公式（a+b）2=（a-b）2+4ab、（a-b）2=（a+b）2-4ab计算即可．
解答 解：∵x2+mx+4=（x±2）2，
即x2+mx+4=x2±4x+4，
∴m=±4．
故答案为：±4．
点评 此题主要考查了公式法分解因式，熟记有关完全平方的几个变形公式是解题关键．
练习册系列答案
浙江之星学业水平测试系列答案
高效智能课时作业系列答案
相关题目
3．
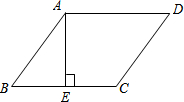如图，在?ABCD中，AE⊥BC于E，AE=EB=EC=a，且a是一元二次方程x2-2x-3=0的根，则?ABCD的周长为（ ）
如图，在?ABCD中，AE⊥BC于E，AE=EB=EC=a，且a是一元二次方程x2-2x-3=0的根，则?ABCD的周长为（ ）| A． | 4+2$\sqrt{2}$ | B． | 12+6$\sqrt{2}$ | C． | 2+2$\sqrt{2}$ | D． | 4+2$\sqrt{2}$或12+6$\sqrt{2}$ |
1．如果□×（-3ab）=9a2b2，则□内应填的代数式是（ ）
| A． | 3ab | B． | -3ab | C． | 3a | D． | -3a |
18．
如图，对比甲、乙两组数据，下列结论中，正确的是（ ）
如图，对比甲、乙两组数据，下列结论中，正确的是（ ）| A． | 甲乙两组数据的方差相等 | B． | 甲组数据的方差较小 | ||
| C． | 乙组数据的方差较大 | D． | 乙组数据的方差较小 |