题目内容
化简代数式(
-
)÷(x+1),再从不等式组
的整数解中选择一个数,求该代数式的值.
| x |
| x-1 |
| 1 |
| x2-x |
|
考点:分式的化简求值,一元一次不等式组的整数解
专题:
分析:先求得不等式组的整数解.然后将其代入化简后的所求代数式进行求值即可.
解答:解:解不等式组,得-1<x≤2.
故不等式组
的整数解是0,1,2.
则(
-
)÷(x+1)=[
-
]÷(x+1)
=
÷(x+1)
=
×
=
.
在原式及化简过程中,x-1、x(x-1)、x+1做为分母,均不能为0.
∴x≠1,且x≠0,且x≠-1,
∴当x=2时,原式=
.
故不等式组
|
则(
| x |
| x-1 |
| 1 |
| x2-x |
| x |
| x-1 |
| 1 |
| x(x-1) |
=
| x2-1 |
| x(x-1) |
=
| (x+1)(x-1) |
| x(x-1) |
| 1 |
| x+1 |
=
| 1 |
| x |
在原式及化简过程中,x-1、x(x-1)、x+1做为分母,均不能为0.
∴x≠1,且x≠0,且x≠-1,
∴当x=2时,原式=
| 1 |
| 2 |
点评:本题考查了分式的化简求值、一元一次不等式组的整数解.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
 如图,为了测出湖两岸A、B之间的距离,观测者在C出设桩,使△ABC恰好为一个直角三角形.通过测量得到AC长为160米,BC长为128米,那么从点A穿过湖到点B的距离为( )
如图,为了测出湖两岸A、B之间的距离,观测者在C出设桩,使△ABC恰好为一个直角三角形.通过测量得到AC长为160米,BC长为128米,那么从点A穿过湖到点B的距离为( )| A、96米 | B、160米 |
| C、86米 | D、90米 |
如图,是用火柴棒按规律拼成的图形,则第6个图形中一共有( )个平行四边形.

| A、6 | B、7 | C、8 | D、9 |
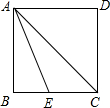 如图,已知:正方形ABCD中,∠BAC的平分线交BC于E,求证:AB+BE=AC.
如图,已知:正方形ABCD中,∠BAC的平分线交BC于E,求证:AB+BE=AC.