题目内容
10.下列条件能判断△ABC与△DEF相似的有( )(1)∠A=∠D,∠E=∠C;(2)$\frac{AB}{AC}=\frac{DE}{DF},∠A=∠D$;(3)$\frac{AB}{DE}=\frac{BC}{EF},∠A=∠D$
(4)$\frac{AB}{DE}=\frac{AC}{DF}=\frac{BC}{EF}$; (5)∠A=∠D,$\frac{BC}{DF}=\frac{2}{3}$.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 直接根据三角形相似的判定方法分别判断得出答案.
解答 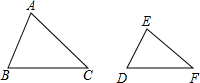 解:(1)∠A=∠D,∠E=∠C,可以得出△ABC∽△DFE,故正确;
解:(1)∠A=∠D,∠E=∠C,可以得出△ABC∽△DFE,故正确;
(2)$\frac{AB}{AC}=\frac{DE}{DF},∠A=∠D$,可以得出△ABC∽△DEF,故正确;
(3)$\frac{AB}{DE}=\frac{BC}{EF},∠A=∠D$,不是两边成比例且夹角相等,故此选项错误;
(4)$\frac{AB}{DE}=\frac{AC}{DF}=\frac{BC}{EF}$,可得出△ABC∽△DEF,故正确;
(5)∠A=∠D,$\frac{BC}{DF}=\frac{2}{3}$,无法得出相似三角形,故此选项错误.
故选:B.
点评 此题主要考查了相似三角形的判定,关键是掌握三角形相似的判定方法:(1)平行线法:平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似;(2)三边法:三组对应边的比相等的两个三角形相似;(3)两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;(4)两角法:有两组角对应相等的两个三角形相似.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.三根木棒的长分别是3cm、4cm和5cm,将他们首尾相接钉成一个三角形.则这个三角形的类型大致是( )
| A. | 直角三角形 | B. | 钝角三角形 | C. | 等腰三角形 | D. | 锐角三角形 |
18.若(x+a)(x+b)的结果中不含有x的一次项,则a、b的关系是( )
| A. | ab=1 | B. | ab=0 | C. | a-b=0 | D. | a+b=0 |
2.算式9÷(-$\frac{3}{5}$)的结果是( )
| A. | -15 | B. | -$\frac{27}{5}$ | C. | 15 | D. | $\frac{27}{5}$ |
19.以下各组数为边长.不能组成三角形的是( )
| A. | 4,5,6 | B. | 7,7,2 | C. | 1,2,3 | D. | 10,11,20 |
 如图,点D在AC上,点E在AB上,AB=AC,∠B=∠C.求证:
如图,点D在AC上,点E在AB上,AB=AC,∠B=∠C.求证: 如图,已知平行四边形ABCD,E为BC的中点,连接BD交AE为F,△BEF的面积为1,BE=3,则平行四边形ABCD的面积为12.
如图,已知平行四边形ABCD,E为BC的中点,连接BD交AE为F,△BEF的面积为1,BE=3,则平行四边形ABCD的面积为12.