题目内容
 如图,有一个横断面为抛物线形的门洞,门洞内地面宽度AB为8m,两侧距地面4m处各有一盏灯,两灯间的水平距离DE为6m.建立适当坐标系,求门洞最高点C距地面的高度.(精确到0.1m)
如图,有一个横断面为抛物线形的门洞,门洞内地面宽度AB为8m,两侧距地面4m处各有一盏灯,两灯间的水平距离DE为6m.建立适当坐标系,求门洞最高点C距地面的高度.(精确到0.1m)考点:二次函数的应用
专题:
分析:由题意可知各点的坐标,A(-4,0),B(4,0),D(-3,4),又由抛物线的顶点在y轴上,即可设抛物线的解析式为y=ax2+c,然后利用待定系数法即可求得此二次函数的解析式,继而求得这个门洞的高度.
解答: 约9.1m解:建立如图所示的平面直角坐标系.
约9.1m解:建立如图所示的平面直角坐标系.
由题意可知各点的坐标,A(-4,0),B(4,0),D(-3,4).
设抛物线的解析式为:y=ax2+c(a≠0),把B(4,0),D(-3,4)代入,得
,
解得
,
∴该抛物线的解析式为:y=-
x2+
,
则C(0,
).
∵
m≈9.1m.
答:门洞的高度是9.1m.
 约9.1m解:建立如图所示的平面直角坐标系.
约9.1m解:建立如图所示的平面直角坐标系.由题意可知各点的坐标,A(-4,0),B(4,0),D(-3,4).
设抛物线的解析式为:y=ax2+c(a≠0),把B(4,0),D(-3,4)代入,得
|
解得
|
∴该抛物线的解析式为:y=-
| 4 |
| 7 |
| 64 |
| 7 |
则C(0,
| 64 |
| 7 |
∵
| 64 |
| 7 |
答:门洞的高度是9.1m.
点评:此题考查了二次函数在实际生活中的应用.题目难度适中,解此题的关键是理解题意,求得相应的函数解析式,注意待定系数法的应用.

练习册系列答案
相关题目
 有一块直角三角形纸片,两直角边AC=12cm,BC=16cm如图,现将直角边AC沿AD折叠,使它落在斜边AB上,且与AE重合,则DE等于( )
有一块直角三角形纸片,两直角边AC=12cm,BC=16cm如图,现将直角边AC沿AD折叠,使它落在斜边AB上,且与AE重合,则DE等于( )| A、6cm | B、8cm |
| C、10cm | D、14cm |
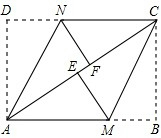 已知:如图,在矩形ABCD中,把∠B、∠D分别翻折,使点B、D分别落在对角线AC上的点E、F处,折痕分别为AN、CM.
已知:如图,在矩形ABCD中,把∠B、∠D分别翻折,使点B、D分别落在对角线AC上的点E、F处,折痕分别为AN、CM. 如图:
如图: