如果x=$\sqrt{5}$+3.y=$\sqrt{5}$-3.那么x2y+xy2=-8$\sqrt{5}$．题目和参考答案——青夏教育精英家教网—

题目内容

16．如果x=$\sqrt{5}$+3，y=$\sqrt{5}$-3，那么x²y+xy²=-8$\sqrt{5}$．

分析根据x=$\sqrt{5}$+3，y=$\sqrt{5}$-3，得出x+y和xy的值，再对要求的式子进行因式分解，然后代值计算即可得出答案．

解答解：∵x=$\sqrt{5}$+3，y=$\sqrt{5}$-3，
∴x+y=$\sqrt{5}$+3+$\sqrt{5}$-3=2$\sqrt{5}$，xy=（$\sqrt{5}$+3）（$\sqrt{5}$-3）=5-9=-4，
∴x²y+xy²=xy（x+y）=-4×2$\sqrt{5}$=-8$\sqrt{5}$；
故答案为：-8$\sqrt{5}$．

点评此题主要考查了二次根式的化简求值，用到的知识点是提取公因式法和完全平方公式的应用，正确将原式变形是解题的关键．

练习册系列答案

相关题目

8．

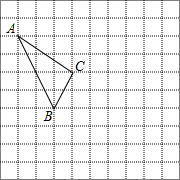在如图所示的正方形网格中，每个小正方形的边长为1，格点三角形（顶点是网格线的交点的三角形）ABC的顶点A、C的坐标分别为（-4，4），（-1，2）．
（1）请在如图所示的网格平面内作出平面直角坐标系；
（2）将△ABC向右平移2个单位长度，然后再向下平移3个单位长度，得到△A′B′C′，画出平移后的△A′B′C′．
（3）写出点△A′B′C′各个顶点的坐标．

9．

如图是由5个相同的小正方体组成的立体图形，它的左视图是（　　）

4．已知y+3与5x+4成正比例，当x=1时，y=-18
（1）求y关于x的函数关系式；
（2）若点（m，-8）在此图象上，求m的值．

11．已知x=$\sqrt{2}$+1，y=$\sqrt{2}$-1，则x²-5xy+y²+6=7．

1．

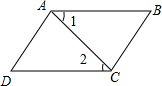如图，已知∠1=∠2，∠BAD=∠BCD，则下列结论：①AB∥CD；②AD∥BC；③∠B=∠D；④∠D=∠ACB，其中正确的有①②③．

8．已知函数$y=\sqrt{2-x}$，则x的取值范围是x≤2．

5．

如图，已知函数y₁=k₁x+b₁和y₂=k₂x+b₂交于点（-3，1），k₁＞0，k₂＜0，如k₁x+b₁＜k₂x+b₂，则x的范围为x＜-3．

6．一水库的水位在最近6天内持续上涨，如表记录了这6天的水位高的：

n（天）	0	1	2	3	4	5	6
h（m）	12	12.5	13	13.5	14	14.5	15

（1）由记录表推出这6天中水位高度h（m）随时间n（天）变化的函数解析式，并画出函数的图象；
（2）据估计这种上涨的势头还会持续2天，预测再过2天水位高度将达到多少米．

试题分类