题目内容
18.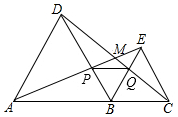 如图,点A、B、C在一条直线上,△ABD、△BCE均为等边三角形,连接AE和CD,AE分别交BD、CD于点P、M,CD交BE于点Q,连接PQ.
如图,点A、B、C在一条直线上,△ABD、△BCE均为等边三角形,连接AE和CD,AE分别交BD、CD于点P、M,CD交BE于点Q,连接PQ.求证:(1)∠DMA=60°;
(2)△BPQ为等边三角形.
分析 (1)根据等边三角形的性质,可证明△ABE≌△DBC,可求得∠BAE=∠BDC,则可证得∠ABD=∠DMA=60°;
(2)由等边三角形的性质,结合(1)中的结论可证明△ABP≌△DBQ,可得BP=BQ,则可证得结论.
解答 证明:
(1)∵△ABD、△BCE均为等边三角形,
∴AB=DB,EB=CB,∠ABD=∠EBC=60°,
∴∠ABD+∠DBE=∠EBC+∠DBE,
即∠ABE=∠DBC,
在△ABE和△DBC中
$\left\{\begin{array}{l}{AB=DB}\\{∠BAE=∠BDC}\\{EB=CB}\end{array}\right.$
∴△ABE≌△DBC (SAS),
∴∠BAE=∠BDC,
在△ABP和△DMP中,
∠BAE=∠BDC,∠APB=∠DPM,
∴∠DMA=∠ABD=60°;
(2)∵△ABD、△BCE均为等边三角形,
∴AB=DB,∠ABD=∠EBC=60°,
∵点A、B、C在一条直线上,
∴∠DBE=60°,
即∠ABD=∠DBE,
由(1)得∠BAE=∠BDC,
在△ABP和△DBQ中
$\left\{\begin{array}{l}{∠ABD=∠EBC}\\{AB=DB}\\{∠BAE=∠BDC}\end{array}\right.$
∴△ABP≌△DBQ(ASA),
∴BP=BQ,
∴△BPQ为等边三角形.
点评 本题主要考查全等三角形的判定和性质及等边三角形的性质,掌握全等三角形的判定方法(即SSS、SAS、ASA、AAS和HL)和全等三角形的性质(即对应边相等、对应角相等)是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.已知一个角的余角是20°,则这个角的补角是( )
| A. | 70° | B. | 80° | C. | 110° | D. | 120° |
13.下列图形中,不是轴对称图形的是( )
| A. | 正方形 | B. | 等腰直角三角形 | ||
| C. | 等边三角形 | D. | 含30°的直角三角形 |
3.下列各组数据中,不能构成直角三角形的三边的是( )
| A. | 3,4,5 | B. | 9,41,40 | C. | 6,3,5 | D. | 13,12,5 |
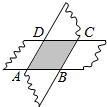 如图,剪两张对边平行的纸条,随意交又叠放在一起,重合的部分构成了一个四边形,转动其中一张纸条,线段AD和BC什么关系?为什么?
如图,剪两张对边平行的纸条,随意交又叠放在一起,重合的部分构成了一个四边形,转动其中一张纸条,线段AD和BC什么关系?为什么?