题目内容
20.解方程组(1)$\left\{\begin{array}{l}{3x+4y=15}\\{2x-4y=10}\end{array}\right.$
(2)$\left\{\begin{array}{l}{x+2y=4}\\{x+y=1}\end{array}\right.$
(3)$\left\{\begin{array}{l}{\frac{x+y}{3}+\frac{x-y}{2}=6}\\{3(x+y)-2(x-y)=28}\end{array}\right.$
(4)$\left\{\begin{array}{l}{x+y+z=12}\\{x+2y-z=6}\\{3x-y+z=10}\end{array}\right.$.
分析 (1)方程利用加减消元法求出解即可;
(2)方程组利用加减消元法求出解即可;
(3)方程组整理后,利用加减消元法求出解即可;
(4)方程组利用加减消元法求出解即可.
解答 解:(1)$\left\{\begin{array}{l}{3x+4y=15①}\\{2x-4y=10②}\end{array}\right.$,
①+②得:5x=25,即x=5,
把x=5代入①得:y=0,
则方程组的解为$\left\{\begin{array}{l}{x=5}\\{y=0}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{x+2y=4①}\\{x+y=1②}\end{array}\right.$,
①-②得:y=3,
把y=3代入②得:x=-2,
则方程组的解为$\left\{\begin{array}{l}{x=-2}\\{y=3}\end{array}\right.$;
(3)方程组整理得:$\left\{\begin{array}{l}{5x-y=36①}\\{x+5y=28②}\end{array}\right.$,
①×5+②得:26x=208,即x=8,
把x=8代入②得:y=4,
则方程组的解为$\left\{\begin{array}{l}{x=8}\\{y=4}\end{array}\right.$;
(4)$\left\{\begin{array}{l}{x+y+z=12①}\\{x+2y-z=6②}\\{3x-y+z=10③}\end{array}\right.$,
①+②得:2x+3y=18④,
②+③得:4x+y=16⑤,
④×2-⑤得:5y=20,即y=4,
把y=4代入④得:x=3,
把x=3,y=4代入①得:z=5.
则方程组的解为$\left\{\begin{array}{l}{x=3}\\{y=4}\\{z=5}\end{array}\right.$.
点评 此题考查了解二元一次方程,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

| A. | 点A在⊙O外 | B. | 点A在⊙O上 | C. | 点A在⊙O 内 | D. | 不能确定 |
| A. | 如果a>b,那么|a|>|b| | B. | 一个角的补角大于这个角 | ||
| C. | 平方后等于4的数是2 | D. | 直角三角形的两个锐角互余 |

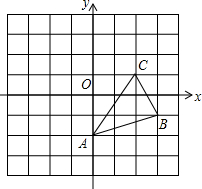 将图中的△ABC作下列变换,画出相应的图形,指出三个顶点的坐标所发生的变化.
将图中的△ABC作下列变换,画出相应的图形,指出三个顶点的坐标所发生的变化.