题目内容
10.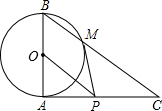 如图,在△ABC中,∠BAC=90°,以AB为直径的⊙O交BC于点M,线段AB=2,AC=2$\sqrt{3}$,过点M的切线交AC边于点P,连接OP.
如图,在△ABC中,∠BAC=90°,以AB为直径的⊙O交BC于点M,线段AB=2,AC=2$\sqrt{3}$,过点M的切线交AC边于点P,连接OP.(1)求sin∠CMP的值;
(2)求证:AP=PC.
分析 (1)连结OM、AM,如图,利用正切定义可计算出∠C=30°,再根据圆周角定理得∠AMB=90°,则∠CAM=60°,接着证明PA为⊙O的切线,而PM为⊙O的切线,根据切线长定理得PM=PA,所以∠PMA=∠PAM=60°,于是可计算出∠CMP=30°,然后根据特殊角的三角函数值求解;
(2)由∠C=∠CMP=30°得到PM=PC,加上PA=PM,所以PA=PC.
解答 (1)解:连结OM、AM,如图,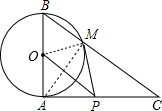 ∵∠BAC=90°,
∵∠BAC=90°,
∴tanC=$\frac{AB}{AC}$=$\frac{2}{2\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
∴∠C=30°,
∵AB为直径,
∴∠AMB=90°,
∴∠CAM=60°,
∵∠BAC=90°,AB为直径,
∴PA为⊙O的切线,
而PM为⊙O的切线,
∴PM=PA,
∴∠PMA=∠PAM=60°,
∴∠CMP=90°-60°=30°,
∴sin∠CMP=sin30°=$\frac{1}{2}$;
(2)证明:∵∠C=∠CMP=30°,
∴PM=PC,
而PA=PM,
∴PA=PC.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了圆周角定理.

练习册系列答案
相关题目
20.下面是第五次全国人口普查我国四个直辖市的人口的两幅统计图.由统计图得到的下列结论你认为正确的是( )
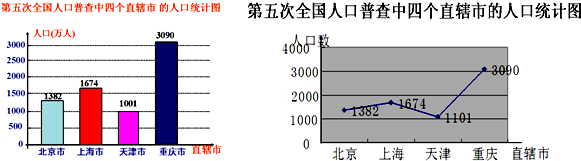

| A. | 重庆的人口与其它三个直辖市人口的和相当 | |
| B. | 重庆的人口增长最快 | |
| C. | 上海相对北京的人口增长的百分数与北京相对天津的人口增长的百分数较小 | |
| D. | 重庆是天津人口总数的3倍还要多 |
5.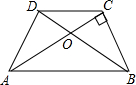 如图,在等腰梯形ABCD中,AB∥CD,对角线AC、BD相交于点O,∠ABD=30°,AC⊥BC,AB=12cm,则△COD的面积为( )
如图,在等腰梯形ABCD中,AB∥CD,对角线AC、BD相交于点O,∠ABD=30°,AC⊥BC,AB=12cm,则△COD的面积为( )
 如图,在等腰梯形ABCD中,AB∥CD,对角线AC、BD相交于点O,∠ABD=30°,AC⊥BC,AB=12cm,则△COD的面积为( )
如图,在等腰梯形ABCD中,AB∥CD,对角线AC、BD相交于点O,∠ABD=30°,AC⊥BC,AB=12cm,则△COD的面积为( )| A. | 4cm2 | B. | 3$\sqrt{3}$cm2 | C. | 4$\sqrt{3}$cm2 | D. | $\frac{4}{3}$$\sqrt{3}$cm2 |
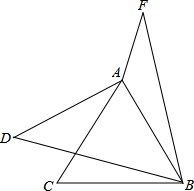 如图,已知等边△ABC,点D在AC的外侧,将BD绕点B顺时针旋转60°至BF,点F与点D相对应,连接AF,AD,AD=2,∠CBD=15°,∠AFB=30°,则AF的长为$\sqrt{6}-\sqrt{2}$.
如图,已知等边△ABC,点D在AC的外侧,将BD绕点B顺时针旋转60°至BF,点F与点D相对应,连接AF,AD,AD=2,∠CBD=15°,∠AFB=30°,则AF的长为$\sqrt{6}-\sqrt{2}$.