题目内容
15.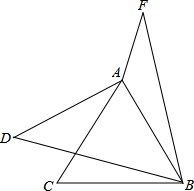 如图,已知等边△ABC,点D在AC的外侧,将BD绕点B顺时针旋转60°至BF,点F与点D相对应,连接AF,AD,AD=2,∠CBD=15°,∠AFB=30°,则AF的长为$\sqrt{6}-\sqrt{2}$.
如图,已知等边△ABC,点D在AC的外侧,将BD绕点B顺时针旋转60°至BF,点F与点D相对应,连接AF,AD,AD=2,∠CBD=15°,∠AFB=30°,则AF的长为$\sqrt{6}-\sqrt{2}$.
分析 通过作辅助线得到等边三角形,由角的度数知道EF是角的平分线,根据三线合一得到线段的垂直平分线,于是得到△DAB是等腰直角三角形,求得DE,AE的长度,也就求出了DF,再由勾股定理求得EF,从而求出AF.
解答 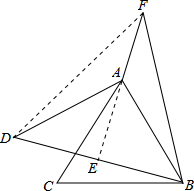 解:连接DF,延长FA交BD于E,
解:连接DF,延长FA交BD于E,
∵BD绕点B顺时针旋转60°至BF,
∴BD=BF,∠DBF=60°,
∴△BDF是等边三角形,
∴∠BFD=60°,
∵∠BFA=30°,
∴∠DFA=30°,
∴FE垂直平分BD,
∴AD=AB,∵∠ABC=60°∠CBD=15°,
∴∠ABD=45°,
∴△DAB是等腰直角三角形,
∴DE=AE=$\frac{\sqrt{2}}{2}$AD=$\sqrt{2}$,
∴BD=DF=2$\sqrt{2}$,
∴EF=$\sqrt{{DF}^{2}{-DE}^{2}}$=$\sqrt{6}$,
∴AF=EF-AE=$\sqrt{6}$-$\sqrt{2}$,
故答案:$\sqrt{6}$-$\sqrt{2}$.
点评 本题考查了旋转的性质,等边三角形的判定和性质,等腰直角三角形的判定和性质,等腰三角形的性质三线合一,勾股定理的应用等知识点.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目

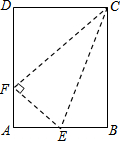 如图,已知矩形ABCD的两边AB与BC的比为4:5,E是AB上的一点,沿CE将△EBC向上翻折,若B点恰好落在边AD上的F点,则tan∠DCF=$\frac{3}{4}$.
如图,已知矩形ABCD的两边AB与BC的比为4:5,E是AB上的一点,沿CE将△EBC向上翻折,若B点恰好落在边AD上的F点,则tan∠DCF=$\frac{3}{4}$.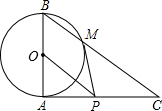 如图,在△ABC中,∠BAC=90°,以AB为直径的⊙O交BC于点M,线段AB=2,AC=2$\sqrt{3}$,过点M的切线交AC边于点P,连接OP.
如图,在△ABC中,∠BAC=90°,以AB为直径的⊙O交BC于点M,线段AB=2,AC=2$\sqrt{3}$,过点M的切线交AC边于点P,连接OP.