题目内容
1.已知抛物线y=3ax2+2bx+c(1)若a=b=1,c=-1,则该抛物线与x轴的交点坐标(-1,0)和($\frac{1}{3}$,0)
(2)若a=$\frac{1}{3}$,c=2+b且抛物线在-2≤x≤2区间上的最小值是-3,则b=3;
(3)若a+b+c=1,存在实数x,使得相应的y的值为1.
请你判断以上三个命题的真假,并说出理由.
分析 (1)把a=b=1,c=-1代入y=3ax2+2bx+c化为y=3x2+2x-1,令y=0,解方程即可求得抛物线与x轴公共点的坐标是:(-1,0)和($\frac{1}{3}$,0),是真命题;
(2)a=$\frac{1}{3}$,c-b=2,则抛物线可化为:y=x2+2bx+b+2,其对称轴为:x=-b,然后三种情况讨论抛物线的最小值,从而得出b=3或b=$\frac{1-\sqrt{21}}{2}$时,最小值是-3,故是假命题;
(3)由y=1得3ax2+2bx+c=1,然后根据△的值即可判定是真命题.
解答 解:(1)当a=b=1,c=-1时,抛物线为:y=3x2+2x-1,
∵方程3x2+2x-1=0的两个根为:x1=-1,x2=$\frac{1}{3}$.
∴该抛物线与x轴公共点的坐标是:(-1,0)和($\frac{1}{3}$,0);
(2)a=$\frac{1}{3}$,c-b=2,则抛物线可化为:y=x2+2bx+b+2,
其对称轴为:x=-b,
当x=-b<-2时,即b>2,则有抛物线在x=-2时取最小值为-3,
此时-3=(-2)2+2×(-2)b+b+2,
解得:b=3,符合题意,
当x=-b>2时,即b<-2,则有抛物线在x=2时取最小值为-3,此时-3=22+2×2b+b+2,
解得:b=-$\frac{9}{5}$,不合题意,舍去.
当-2≤-b≤2时,即-2≤b≤2,则有抛物线在x=-b时,取最小值为-3,
此时-3=(-b)2+2×(-b)b+b+2,
化简得:b2-b-5=0,
解得:b1=$\frac{1+\sqrt{21}}{2}$(不合题意,舍去),b2=$\frac{1-\sqrt{21}}{2}$.
综上:b=3或b=$\frac{1-\sqrt{21}}{2}$;
(3)由y=1得3ax2+2bx+c=1,
△=4b2-12a(c-1),
=4b2-12a(-a-b),
=4b2+12ab+12a2,
=4(b2+3ab+3a2),
=4[(b+$\frac{3}{2}$a)2+$\frac{3}{4}$a2],
∵a≠0,△>0,
所以方程3ax2+2bx+c=1有两个不相等实数根,
即存在两个不同实数x,使得相应y=1.
所以真命题为(1)(3),假命题为(2).
点评 本题考查了二次函数与x轴的交点,抛物线的顶点,以及二次方程的根的情况,熟练掌握二次函数的性质是解题的关键.

 如图,关于抛物线y=x2+2x-1,下列说法错误的是( )
如图,关于抛物线y=x2+2x-1,下列说法错误的是( )| A. | 顶点坐标为(-1,-2) | B. | 对称轴是直线x=-l | ||
| C. | 开口方向向上 | D. | 当x>-1时,y随x的增大而减小 |
 如图,四边形ABCD∽四边形A1B1C1D1,AB=12,CD=15,A1B1=9,则边C1D1的长是( )
如图,四边形ABCD∽四边形A1B1C1D1,AB=12,CD=15,A1B1=9,则边C1D1的长是( )| A. | 10 | B. | 12 | C. | $\frac{45}{4}$ | D. | $\frac{36}{5}$ |
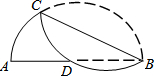 将弧BC沿弦BC折叠,交直径AB于点D,若AD=8,DB=10,则BC的长是( )
将弧BC沿弦BC折叠,交直径AB于点D,若AD=8,DB=10,则BC的长是( )| A. | 6$\sqrt{7}$ | B. | 16 | C. | 2$\sqrt{65}$ | D. | 4$\sqrt{15}$ |
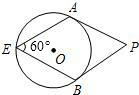 如图,点E是半径为6的⊙O上一点,过点E作一只60°的圆周角∠AEB,分别过点A、B作⊙O的切线,两条切线交于点P.那么四边形AEBP的面积的最大值是54$\sqrt{3}$.
如图,点E是半径为6的⊙O上一点,过点E作一只60°的圆周角∠AEB,分别过点A、B作⊙O的切线,两条切线交于点P.那么四边形AEBP的面积的最大值是54$\sqrt{3}$.
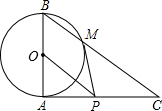 如图,在△ABC中,∠BAC=90°,以AB为直径的⊙O交BC于点M,线段AB=2,AC=2$\sqrt{3}$,过点M的切线交AC边于点P,连接OP.
如图,在△ABC中,∠BAC=90°,以AB为直径的⊙O交BC于点M,线段AB=2,AC=2$\sqrt{3}$,过点M的切线交AC边于点P,连接OP. 观察如图规律,则A等于40.
观察如图规律,则A等于40.