题目内容
18.不解方程,一元二次方程x2-3x=5的根的情况是原方程有两个不相等的实数根.分析 把a=1,b=-3,c=-5代入判别式△=b2-4ac进行计算,然后根据计算结果判断根的情况.
解答 解:∵a=1,b=-3,c=-5,
∴△=b2-4ac=(-3)2-4×1×(-5)=29>0,
∴方程有两个不相等的实数根.
故答案为:原方程有两个不相等的实数根.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)根的判别式△=b2-4ac.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
相关题目
13.检查一个门框是矩形的方法是( )
| A. | 测量两条对角线是否相等 | B. | 测量有三个角是直角 | ||
| C. | 测量两条对角线是否互相平分 | D. | 测量两条对角线是否互相垂直 |
7.已知$\frac{x}{{{x^2}+x+1}}=\frac{1}{8}$(0<x<1).则$\sqrt{x}-\frac{1}{{\sqrt{x}}}$的值为( )
| A. | $-\sqrt{7}$ | B. | $\sqrt{7}$ | C. | $-\sqrt{5}$ | D. | $\sqrt{5}$ |
 已知AB=AC,AD=AE,∠BAC=∠DAE,直线BD、CE交于点G,
已知AB=AC,AD=AE,∠BAC=∠DAE,直线BD、CE交于点G,
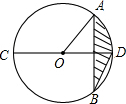 如图,CD是⊙O的直径,弦AB⊥CD,∠ABD=30°,若$CD=2\sqrt{6}$,则阴影部分图形的面积为π.
如图,CD是⊙O的直径,弦AB⊥CD,∠ABD=30°,若$CD=2\sqrt{6}$,则阴影部分图形的面积为π.