题目内容
14. 如图,在⊙O中,两弦AB与CD的中点分别是P,Q,且$\widehat{AB}$=$\widehat{CD}$,连接PQ.求证:∠APQ=∠CQP.
如图,在⊙O中,两弦AB与CD的中点分别是P,Q,且$\widehat{AB}$=$\widehat{CD}$,连接PQ.求证:∠APQ=∠CQP.
分析 连接OP,OQ,根据圆心角,弧,弦的关系得到AB=CD,根据垂径定理得到OP⊥AB,OQ⊥CD,于是得到OP=OQ,∠APO=∠CQO=90°,由等腰三角形的性质得到∠OPQ=∠OQP,即可得到结论.
解答  解:连接OP,OQ,
解:连接OP,OQ,
∵$\widehat{AB}$=$\widehat{CD}$,
∴AB=CD,
∵两弦AB与CD的中点分别是P,Q,
∴OP⊥AB,OQ⊥CD,
∴OP=OQ,∠APO=∠CQO=90°,
∴∠OPQ=∠OQP,
∴∠APQ=∠CQP.
点评 本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.一元一次方程$\frac{x}{1×2}$+$\frac{x}{2×3}$+$\frac{x}{3×4}$+…+$\frac{x}{2015×2016}$=2015的解是( )
| A. | 2014 | B. | 2015 | C. | 2016 | D. | 2017 |
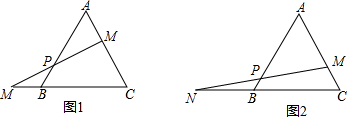
 如图,在△ABC中,点D为边AB上一点,点F为BC延长线上一点,且AD=CF,连结DF,与AC相交于点E,点G为AC上一点,DG∥BC,△ADG∽△ABC,△EDG∽△EFC,那么$\frac{AB}{BC}$=$\frac{EF}{DE}$吗?为什么?
如图,在△ABC中,点D为边AB上一点,点F为BC延长线上一点,且AD=CF,连结DF,与AC相交于点E,点G为AC上一点,DG∥BC,△ADG∽△ABC,△EDG∽△EFC,那么$\frac{AB}{BC}$=$\frac{EF}{DE}$吗?为什么? 如图,为测量某建筑物的高度,在离该建筑物底部30.0米处,目测其顶,视线与水平线的夹角为40°,目高为1.5米.试利用相似三角形的知识,求出该建筑物的高度.(精确到0.1米)
如图,为测量某建筑物的高度,在离该建筑物底部30.0米处,目测其顶,视线与水平线的夹角为40°,目高为1.5米.试利用相似三角形的知识,求出该建筑物的高度.(精确到0.1米)