题目内容
20. 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(-1,0),对称轴为直线x=2,下列结论:(1)c>0;(2)4a+b=0;(3)9a+c>3b;(4)8a+7b+2c>0;(5)若点A(-3,y1)、点B(-$\frac{1}{2}$,y2)、点C($\frac{7}{2}$,y3)在该函数图象上,则y1<y3<y2;(6)若方程a(x+1)(x-5)=-3的两根为x1和x2,且x1<x2,则x1<-1<5<x2.其中正确的结论有( )
二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(-1,0),对称轴为直线x=2,下列结论:(1)c>0;(2)4a+b=0;(3)9a+c>3b;(4)8a+7b+2c>0;(5)若点A(-3,y1)、点B(-$\frac{1}{2}$,y2)、点C($\frac{7}{2}$,y3)在该函数图象上,则y1<y3<y2;(6)若方程a(x+1)(x-5)=-3的两根为x1和x2,且x1<x2,则x1<-1<5<x2.其中正确的结论有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 抛物线交y轴于正半轴,c>0,根据抛物线的对称轴为直线x=2,则有4a+b=0;观察函数图象得到当x=-3时,函数值小于0,则9a-3b+c<0,即9a+c<3b;由于x=-1时,y=0,则a-b+c=0,易得c=-5a,所以8a+7b+2c=8a-28a-10a=-30a,再根据抛物线开口向下得a<0,于是有8a+7b+2c>0;利用抛物线的对称性得到($\frac{1}{2}$,y3),然后利用二次函数的增减性求解即可,作出直线y=-3,然后依据函数图象进行判断即可.
解答 解:∵抛物线交y轴于正半轴,c>0,故①正确.
∵x=-$\frac{b}{2a}$=2,
∴4a+b=0,故②正确.
由函数图象可知:当x=-3时,y<0,即9a-3b+c<0,
∴9a+c<3b,故③错误.
∵抛物线与x轴的一个交点为(-1,0),
∴a-b+c=0
又∵b=-4a,
∴a+4a+c=0,即c=-5a,
∴8a+7b+2c=8a-28a-10a=-30a,
∵抛物线开口向下,
∴a<0,
∴8a+7b+2c>0,故④正确;
∵抛物线的对称轴为x=2,C($\frac{7}{2}$,y3),
∴($\frac{1}{2}$,y3).
∵-3<-$\frac{1}{2}$<$\frac{1}{2}$,在对称轴的左侧,
∴y随x的增大而增大,
∴y1<y2<y3,故⑤错误.
方程a(x+1)(x-5)=0的两根为x=-1或x=5,
过y=-3作x轴的平行线,直线y=-3与抛物线的交点的横坐标为方程的两根,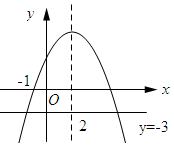
依据函数图象可知:x1<-1<5<x2.故⑥正确,
故答案为:①②④⑥.
故选C.
点评 本题主要考查的是二次函数的图象与系数的关系、抛物线与x轴的交点,熟练掌握二次函数的性质以及数学结合是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.下列图形中,不是中心对称图形的为( )
| A. |  | B. |  | C. |  | D. |  |
11.某班开展以“提倡勤俭节约,反对铺张浪费”为主题教育活动.为了解学生每天使用零花钱的情况,小明随机调查了10名同学,结果如下表:
关于这10名同学每天使用的零花钱,下列说法正确的是( )
| 每天使用零花钱(单位:元) | 0 | 2 | 3 | 4 | 5 |
| 人数 | 1 | 2 | 4 | 1 | 2 |
| A. | A、平均数是3 | B. | 中位数是4 | C. | 众数是2 | D. | 方差是4 |
5. 如图,能判定AC∥BD的条件是( )
如图,能判定AC∥BD的条件是( )
 如图,能判定AC∥BD的条件是( )
如图,能判定AC∥BD的条件是( )| A. | ∠A=∠DBC | B. | ∠A=∠D | C. | ∠A=∠DCE | D. | ∠A+∠ABD=180° |