题目内容
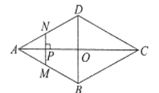
【题目】在菱形ABCD中,点P是BC边上一点,连接AP,点E,F是AP上的两点,连接DE,BF,使得∠AED=∠ABC,∠ABF=∠BPF.
求证:(1)△ABF≌△DAE;
(2)DE=BF+EF.

【答案】(1)见解析;(2)见解析.
【解析】
(1)根据菱形的性质得到AB=AD,AD∥BC,由平行线的性质得到∠BPA=∠DAE,等量代换得到∠BAF=∠ADE,求得∠ABF=∠DAE,根据全等三角形的判定定理即可得到结论;
(2)根据全等三角形的性质得到AE=BF,DE=AF,根据线段的和差即可得到结论
证明:(1)∵四边形ABCD是菱形,
∴AB=AD,AD∥BC,
∴∠BPA=∠DAE,
∵∠ABC=∠AED,
∴∠BAF=∠ADE,
∵∠ABF=∠BPF,∠BPA=∠DAE,
∴∠ABF=∠DAE,
∵AB=DA,
∴△ABF≌△DAE(ASA);
(2)∵△ABF≌△DAE,
∴AE=BF,DE=AF,
∵AF=AE+EF=BF+EF,
∴DE=BF+EF.

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案【题目】某中学开展黄梅戏演唱比赛,组委会将本次比赛的成绩(单位:分)进行整理,并绘制成如下频数分布表和频数分布直方图(不完整).
成绩 | 频数 | 频率 |
| 2 | 0.04 |
|
| 0.16 |
| 20 | 0.40 |
| 16 | 0.32 |
| 4 |
|
合计 | 50 | 1 |
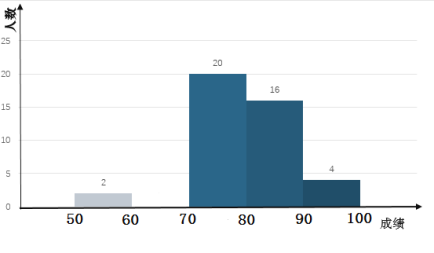
请你根据图表提供的信息,解答下列问题:
(1)求出![]() ,
,![]() 的值并补全频数分布直方图.
的值并补全频数分布直方图.
(2)将此次比赛成绩分为三组:![]() ;
;![]() ;
;![]() 若按照这样的分组方式绘制扇形统计图,则其中
若按照这样的分组方式绘制扇形统计图,则其中![]() 组所在扇形的圆心角的度数是多少?
组所在扇形的圆心角的度数是多少?
(3)学校准备从不低于90分的参赛选手中任选2人参加市级黄梅戏演唱比赛,求都取得了95分的小欣和小怡同时被选上的概率.
【题目】我国正在逐步进入人口老龄化社会,某市老龄化社会研究机构经过抽样调查,发现当地老年人的日常休闲方式主要有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 五种类型,抽样调查的统计结果如下表,则下列说法不正确的是( )
五种类型,抽样调查的统计结果如下表,则下列说法不正确的是( )
休闲类型 | 休闲方式 | 人数 |
| 老年大学 |
|
| 老年合唱队 |
|
| 老年舞蹈队 |
|
| 太极拳 |
|
| 其它方式 |
|
A.当地老年人选择![]() 型休闲方式的人数最少
型休闲方式的人数最少
B.当地老年人选择![]() 型休闲方式的频率是
型休闲方式的频率是![]()
C.估计当地![]() 万名老年人中约有
万名老年人中约有![]() 万人选择
万人选择![]() 型休闲方式
型休闲方式
D.这次抽样调查的样本容量是![]()