题目内容
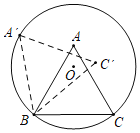
【题目】如图,正![]() 的边长为2,顶点
的边长为2,顶点![]() 、
、![]() 在半径为
在半径为![]() 的圆上,顶点
的圆上,顶点![]() 在圆内,将正
在圆内,将正![]() 绕点
绕点![]() 逆时针旋转,当点
逆时针旋转,当点![]() 第一次落在圆上时,则点
第一次落在圆上时,则点![]() 运动的路线长为__________(结果保留
运动的路线长为__________(结果保留![]() );若
);若![]() 点落在圆上记做第1次旋转,将
点落在圆上记做第1次旋转,将![]() 绕点
绕点![]() 逆时针旋转,当点
逆时针旋转,当点![]() 第一次落在圆上记做第2次旋转,再绕
第一次落在圆上记做第2次旋转,再绕![]() 将
将![]() 逆时针旋转,当点
逆时针旋转,当点![]() 第一次落在圆上,记做第3次旋转……,若此旋转下去,当
第一次落在圆上,记做第3次旋转……,若此旋转下去,当![]() 完成第2018次旋转时,
完成第2018次旋转时,![]() 边共回到原来位置__________次.
边共回到原来位置__________次.
【答案】![]() 168
168
【解析】
首先连接OA′、OB、OC,再求出∠C′BC的大小,进而利用弧长公式问题即可解决.因为△ABC是三边在正方形CBA′C″上,BC边每12次回到原来位置,2018÷12=168.166……,推出当△ABC完成第2018次旋转时,BC边共回到原来位置168次.
解:如图,连接OA′、OB、OC.
∵OB=OC=![]()
,BC=2,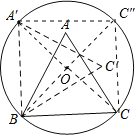
∴△OBC是等腰直角三角形,
∴∠OBC=45°;
同理可证:∠OBA′=45°,
∴∠A′BC=90°;
∵∠ABC=60°,
∴∠A′BA=90°-60°=30°,
∴∠C′BC=∠A′BA=30°,
∴当点A第一次落在圆上时,则点C运动的路线长为:![]() =
=![]() .
.
∵△ABC是三边在正方形CBA′C″上,BC边每12次回到原来位置,
2018÷12=168.166……,
∴当△ABC完成第2018次旋转时,BC边共回到原来位置168次,
故答案为:![]() ,168.
,168.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目