题目内容
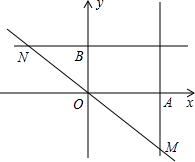
函数y=- x2+3的图象与x轴正半轴交于点A,与y轴交于点B,过点A、B分别作y轴、x轴的平行线交直线y=kx于点M、N.
x2+3的图象与x轴正半轴交于点A,与y轴交于点B,过点A、B分别作y轴、x轴的平行线交直线y=kx于点M、N.
(1)用k表示S△OBN:S△MAO的值.
(2)当S△OBN= S△MAO时,求图象过点M、N、B的二次函数的解析式.
S△MAO时,求图象过点M、N、B的二次函数的解析式.
 解:(1)由y=-
解:(1)由y=- x2+3知:点A(4,0)、B(0,3);
x2+3知:点A(4,0)、B(0,3);当x=4时,y=kx=4k,即:M(4,4k);
当y=3时,kx=3,x=
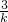 ,即:N(
,即:N(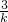 ,3);
,3);∴AM=4|k|、BN=
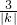 ;
;∴S△OBN=
 OB•BN=
OB•BN= •3•
•3•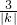 =
=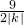 ,S△MAO=
,S△MAO= •OA•AM=
•OA•AM= •4•4|k|=8|k|;
•4•4|k|=8|k|;∴
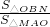 =
=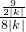 =
=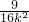 .
.(2)由S△OBN=
 S△MAO,得:
S△MAO,得: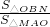 =
= ,即:
,即: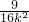 =
= ,解得:k=±
,解得:k=± ;
;当k=
 时,M(4,6)、N(2,3);
时,M(4,6)、N(2,3);设抛物线的解析式为:y=ax2+bx+c,有:
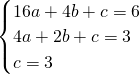 ,解得:
,解得: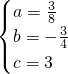
∴抛物线的解析式:y=
 x2-
x2- x+3;
x+3;当k=-
 时,M(4,-6)、N(-2,3),同理可求得抛物线的解析式为:y=-
时,M(4,-6)、N(-2,3),同理可求得抛物线的解析式为:y=- x2-
x2- x+3;
x+3;综上,过点M、N、B的二次函数的解析式为:y=
 x2-
x2- x+3或y=-
x+3或y=- x2-
x2- x+3.
x+3.分析:(1)首先由抛物线的解析式求出点A、B的坐标,进而能得到M、N的坐标,以及AM、BN的长,OA、OB长易知,即可得到△OBN、△OMA的面积表达式,由此得解.
(2)将△OBN、△MAO的面积表达式代入S△OBN=
 S△MAO中,求出k值后即可确定点M、N的坐标,再由待定系数法确定二次函数的解析式.
S△MAO中,求出k值后即可确定点M、N的坐标,再由待定系数法确定二次函数的解析式.点评:此题主要考查了函数解析式的确定、函数图象交点坐标的解法以及图形面积的求法等知识;本题中,k的符号并不明确,因此要防止漏解的情况发生.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
二次函数y=x2-3x的图象不经过( )
| A、第一象限 | B、第二象限 | C、第三象限 | D、第四象限 |
 (2013•奉贤区二模)如图,已知二次函数y=-x2+2mx的图象经过点B(1,2),与x轴的另一个交点为A,点B关于抛物线对称轴的对称点为C,过点B作直线BM⊥x轴垂足为点M.
(2013•奉贤区二模)如图,已知二次函数y=-x2+2mx的图象经过点B(1,2),与x轴的另一个交点为A,点B关于抛物线对称轴的对称点为C,过点B作直线BM⊥x轴垂足为点M.