题目内容
5.已知:∠A,∠B,∠C是△ABC的内角,求证:∠A,∠B,∠C中至多有一个角是钝角.分析 利用反证法的步骤得出答案.
解答 证明:在用反证法证明时,我们首先假设∠A、∠B、∠C中有两个或三个钝角(或∠A、∠B、∠C中至少有两个钝角),然后再去说明我们的假设与三角形内角和定理矛盾,因而假设错误,所以∠A,∠B,∠C中至多有一个角是钝角.
点评 此题主要考查了反证法,反证法的一般步骤是:
①假设命题的结论不成立;
②从这个假设出发,经过推理论证,得出矛盾;
③由矛盾判定假设不正确,从而肯定原命题的结论正确.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
16.已知三角形的两边之长分别为3cm和5cm,则第三边的长可能为( )
| A. | 2cm | B. | 4cm | C. | 8cm | D. | 10cm |
17.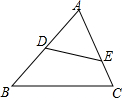 如图,D、E分别为△ABC中AB、AC边上的点,添加一个条件,使△ADE与△ABC相似,添加的条件错误是( )
如图,D、E分别为△ABC中AB、AC边上的点,添加一个条件,使△ADE与△ABC相似,添加的条件错误是( )
 如图,D、E分别为△ABC中AB、AC边上的点,添加一个条件,使△ADE与△ABC相似,添加的条件错误是( )
如图,D、E分别为△ABC中AB、AC边上的点,添加一个条件,使△ADE与△ABC相似,添加的条件错误是( )| A. | ∠B=∠AED | B. | AE•AC=AD•AB | C. | ∠C=∠ADE | D. | $\frac{AE}{AB}=\frac{DE}{BC}$ |
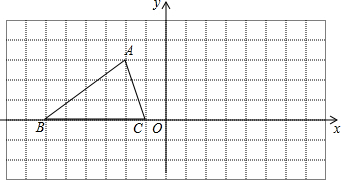 如图所示,已知△ABC的三个顶点的坐标分别为A(-2,3),B(-6,0),C(-1,0).
如图所示,已知△ABC的三个顶点的坐标分别为A(-2,3),B(-6,0),C(-1,0).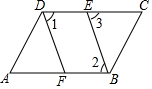 如图,已知在四边形ABCD中,∠ABC=∠ADC,BE、DF分别平分∠ABC和∠ADC,且BE∥DF,求证:∠A=∠C
如图,已知在四边形ABCD中,∠ABC=∠ADC,BE、DF分别平分∠ABC和∠ADC,且BE∥DF,求证:∠A=∠C