题目内容
14.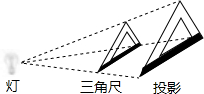 如图,三角尺与其灯光照射下的中心投影组成了位似图形,它们的相似比为2:3,若三角尺的一边长为8cm,则这条边在投影中的对应边长为( )
如图,三角尺与其灯光照射下的中心投影组成了位似图形,它们的相似比为2:3,若三角尺的一边长为8cm,则这条边在投影中的对应边长为( )| A. | 8cm | B. | 12cm | C. | 16cm | D. | 24cm |
分析 利用相似比为2:3,可得出其对应边的比值为2:3,进而求出即可.
解答 解:∵三角尺与其灯光照射下的中心投影组成了位似图形,它们的相似比为2:3,三角尺的一边长为8cm,
∴设这条边在投影中的对应边长为:x,则$\frac{2}{3}$=$\frac{8}{x}$,解得:x=12.
故选:B.
点评 此题主要考查了位似变换,利用相似比得出对应边的比值是解题关键.

练习册系列答案
相关题目
5.下列命题中真命题是( )
| A. | 对角线互相垂直的四边形是矩形 | B. | 对角线相等的四边形是矩形 | ||
| C. | 四条边都相等的四边形是矩形 | D. | 四个内角都相等的四边形是矩形 |
6.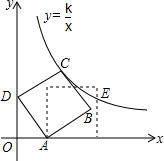 如图,在平面直角坐标系中,边长为2的正方形ABCD斜靠在y轴上,顶点A(1,0),反比例函数y=$\frac{k}{x}$图象经过点C,将正方形ABCD绕点A顺时针旋转一定角度后,使得点B恰好落在x轴的正半轴上,此时边BC交反比例图象于点E,则点E的纵坐标是( )
如图,在平面直角坐标系中,边长为2的正方形ABCD斜靠在y轴上,顶点A(1,0),反比例函数y=$\frac{k}{x}$图象经过点C,将正方形ABCD绕点A顺时针旋转一定角度后,使得点B恰好落在x轴的正半轴上,此时边BC交反比例图象于点E,则点E的纵坐标是( )
 如图,在平面直角坐标系中,边长为2的正方形ABCD斜靠在y轴上,顶点A(1,0),反比例函数y=$\frac{k}{x}$图象经过点C,将正方形ABCD绕点A顺时针旋转一定角度后,使得点B恰好落在x轴的正半轴上,此时边BC交反比例图象于点E,则点E的纵坐标是( )
如图,在平面直角坐标系中,边长为2的正方形ABCD斜靠在y轴上,顶点A(1,0),反比例函数y=$\frac{k}{x}$图象经过点C,将正方形ABCD绕点A顺时针旋转一定角度后,使得点B恰好落在x轴的正半轴上,此时边BC交反比例图象于点E,则点E的纵坐标是( )| A. | $\sqrt{3}$ | B. | $\frac{1}{3}\sqrt{3}+1$ | C. | $\frac{1}{2}\sqrt{3}+1$ | D. | $\frac{3}{2}$ |
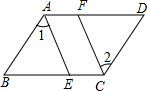 如图,在四边形ABCD中,已知AD∥BC,∠DAB=∠BCD,∠1=∠2,在说明AE∥CF的解答过程中,填上适当的理由.
如图,在四边形ABCD中,已知AD∥BC,∠DAB=∠BCD,∠1=∠2,在说明AE∥CF的解答过程中,填上适当的理由.