题目内容
化简求值:
(1)[(xy+2)(xy-2)-2(x2y2-2)]÷xy,其中x=10,y=-
;
(2)(a-
b)[(a+
b)2-(a-
b)2](a2+
ab+b2)-2b(a4-1),其中a=2,b=-1.
(1)[(xy+2)(xy-2)-2(x2y2-2)]÷xy,其中x=10,y=-
| 1 |
| 25 |
(2)(a-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
考点:整式的混合运算—化简求值
专题:计算题
分析:(1)原式中括号中利用平方差公式计算,去括号合并后,利用多项式除以单项式法则计算得到最简结果,把x与y的值代入计算即可求出值;
(2)原式利用多项式乘以多项式,以及单项式乘以多项式法则计算,去括号合并得到最简结果,把a与b的值代入计算即可求出值.
(2)原式利用多项式乘以多项式,以及单项式乘以多项式法则计算,去括号合并得到最简结果,把a与b的值代入计算即可求出值.
解答:解:(1)原式=(x2y2-4-2x2y2+4)÷xy=-xy,
当x=10,y=-
时,原式=
;
(2)原式=2ab(a-
b)(a2+
ab+b2)-2b(a4-1)=2ab(a3-
b3)-2a4b+2b=2a4b-
ab4-2a4b+2b=-
ab4+2b,
当a=2,b=-1时,原式=-
-2=-2
.
当x=10,y=-
| 1 |
| 25 |
| 2 |
| 5 |
(2)原式=2ab(a-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 8 |
| 1 |
| 4 |
| 1 |
| 4 |
当a=2,b=-1时,原式=-
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题考查了整式的混合运算-化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知⊙O的半径为3,线段OP的长度为2,则点P与⊙O的位置关系是( )
| A、点P在⊙O内 |
| B、点P在⊙O上 |
| C、点P在⊙O外 |
| D、无法确定 |
已知点P(6,-6),Q(-6,-6),则直线PQ( )
| A、平行于x轴 |
| B、平行于y轴 |
| C、不平行于任何坐标轴 |
| D、不能确定 |
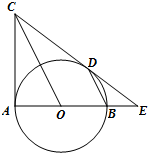 如图,已知AB为⊙O的直径,AC为⊙O的切线,连结CO.BD∥OC交⊙O于D,延长AB、CD交于点E.
如图,已知AB为⊙O的直径,AC为⊙O的切线,连结CO.BD∥OC交⊙O于D,延长AB、CD交于点E.