Question

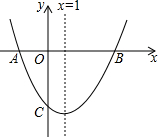如图，已知抛物线y=ax²+bx+c（a≠0）的对称轴为x=1，且抛物线经过A（-1，0）、C（0，-3）两点，与x轴交于另一点B．
（1）求这条抛物线所对应的函数解析式；
（2）在直线BC下方的抛物线上是否在存在一点M，使△MBC的面积最大？若存在，求出点M的坐标；若不存在，请说明理由．
（3）设点P为抛物线的对称轴x=1上一动点，求使△PCB是直角三角形的点P的坐标．（不写过程，直接写出点的坐标）

Answer 1

考点：二次函数综合题

专题：综合题

分析：（1）把A与B两点坐标代入抛物线解析式得到两个方程，由对称轴公式列出方程，联立求出a，b，c的值，即可确定出解析式；
（2）存在，由B与C坐标确定出直线BC斜率，当M为与BC平行且与抛物线的唯一一个交点时，△MBC的面积最大，求出此时M坐标即可；
（3）分三种情况考虑：∠PBC为直角；∠BCP为直角；∠BPC为直角，分别求出P的坐标即可．

解答：解：（1）由题意得：

a-b+c=0 c=-3 - b 2a =1

，
解得：a=1，b=-2，c=-3，
则抛物线解析式为y=x²-2x-3；
（2）存在，当M为与BC平行且与抛物线的唯一一个交点时，△MBC的面积最大，
对于抛物线解析式y=x²-2x-3，
令y=0，得到x²-2x-3=0，即（x-3）（x+1）=0，
解得：x=3或x=-1，
即B（3，0），
∵C（0，-3），
∴直线BC斜率为

-3-0

0-3

=1，
设与直线BC平行的直线解析式为y=x+b，
与抛物线解析式联立得：

y=x+b y=x2-2x-3

，
消去y得：x²-2x-3=x+b，即x²-3x-3-b=0，
当△=0，即9+4（3+b）=0时，抛物线与直线有唯一交点，
解得：b=-

21

4

，即直线为y=x-

21

4

，
方程为x²-3x-3+

21

4

=0，即4x²-12x+9=0，
解得：x=

3

2

，
把x=

3

2

代入得：y=-

15

4

，
则满足题意M坐标为（

3

2

，-

15

4

）；
（3）分三种情况考虑：
当∠PBC为直角时，由直线BC解析式为y=x-3，
过B与直线BC垂直的直线方程为y=-x+3，
把x=1代入得：y=-1+3=2，此时P坐标为（1，2）；
当∠BCP为直角，过C与直线BC垂直的直线方程为y=-x-3，
把x=1代入得：y=-1-3=-4，此时P坐标为（1，-4）；
当∠BPC为直角时，设P（1，p），
此时直线PB斜率为

p-0

1-3

=-

p

2

；直线PC斜率为

p+3

1-0

=p+3，
∵PB⊥PC，∴-

p

2

（p+3）=-1，
解得：p=

-3± 17

2

，此时P坐标为（1，

-3+ 17

2

）或（1，

-3- 17

2

）．

点评：此题属于二次函数综合题，涉及的知识有：待定系数法确定二次函数解析式，一次函数与二次函数的交点，两直线平行时斜率满足的关系，两直线垂直时斜率满足的关系，熟练掌握待定系数法是解本题第一问的关键．