题目内容
如图所示,△ABC中,AB=BC ,DE⊥AB于点E,DF⊥BC于点D,交AC于F

(1)若∠AFD=155,求∠EDF的度数;
(2)若点F是AC的中点,求证:∠CFD= ∠B
∠B
(1)∠EDF=50o;(2)见解析
【解析】
试题分析:(1)先根据等腰三角形等边对等角的性质得到∠B=∠C,利用等角的余角相等和已知角可求出∠EDB的数,从而可求得∠EDF的度数;
(2)利用等腰三角形的三线合一,然后再利用等角的余角相等,即可得出结论
试题解析:(1)∵∠AFD=155o
∴∠DFC=25o
∵DF⊥BC, DE⊥AB
∴∠FDC=∠AED=90o
在Rt△EDC中
∴∠C=90o―25o=65o
∵AB=BC
∴∠C=∠A=65o
∴∠EDF=360o―65o―155o―90o=50o (3分)
(2)连接BF
∵AB=BC,且点F是AC的中点
∴BF⊥AC, ∠ABF=∠CBF= ∠ABC
∠ABC
∴∠CFD+∠BFD=90o
∠CBF+∠BFD=90o
∴∠CFD=∠CBF
∴∠CFD= ∠ABC (6分)
∠ABC (6分)

考点:等腰三角形的性质

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案
相关题目
 是直线
是直线 上异于A,B的一个动点,且满足
上异于A,B的一个动点,且满足 ,则
,则
 一定在射线
一定在射线 上
上 一定在线段
一定在线段 上
上 可以在射线
可以在射线 上,也可以在线段
上,也可以在线段 上
上 可以在射线
可以在射线 上,也可以在线段
上,也可以在线段
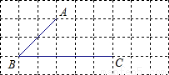
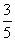 ,则cosB的值是( )
,则cosB的值是( ) B.
B. 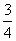 D.
D. 