题目内容
1.已知关于x的方程x2-2(m+2)x+m2-4=0的两个实根互为倒数,m的值是±$\sqrt{5}$.分析 设a、b为方程x2-2(m+2)x+m2-4=0的两个实数根,由两根互为倒数求得m的数值.
解答 解:设a、b为方程x2-2(m+2)x+m2-4=0的两个实数根,
则ab=m2-4=1,
解得:m=±$\sqrt{5}$.
故答案为:±$\sqrt{5}$.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.-$\frac{1}{2}$的相反数是( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | -2 | D. | -$\frac{1}{2}$ |
11.已知二次函数y=ax2+bx+c(a≠0)中自变量x和函数值y的部分对应值如表,求该二次函数解析式的一般形式.
| x | … | -$\frac{3}{2}$ | -1 | -$\frac{1}{2}$ | 0 | $\frac{1}{2}$ | 1 | $\frac{3}{2}$ | … |
| y | … | -$\frac{5}{4}$ | -2 | -$\frac{9}{4}$ | -2 | -$\frac{5}{4}$ | 0 | $\frac{7}{4}$ | … |
 如图,已知△ABC中,CF⊥AB于F,BE⊥AC于F,若S△ABC=36cm2,S△AEF=4cm2,求sinA的值.
如图,已知△ABC中,CF⊥AB于F,BE⊥AC于F,若S△ABC=36cm2,S△AEF=4cm2,求sinA的值.
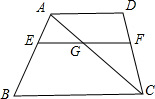 如图,梯形ABCD中,AD∥BC,已知点F是CD的中点,过点F作EF∥AD交AC于点G,交AB于点E,AD=6;
如图,梯形ABCD中,AD∥BC,已知点F是CD的中点,过点F作EF∥AD交AC于点G,交AB于点E,AD=6;