题目内容
19.已知m是方程x2-x-3=0的一个实数根,求代数式(m2-m)(m-$\frac{3}{m}$+1)的值.分析 先根据一元二次方程的解的定义得到m2=m+3,则(m2-m)(m-$\frac{3}{m}$+1)=(m+3-m)•$\frac{{m}^{2}-3+m}{m}$,然后合并后进行乘法运算即可.
解答 解:∵m是方程x2-x-3=0的一个实数根,
∴m2-m-3=0,即m2=m+3,
∴(m2-m)(m-$\frac{3}{m}$+1)=(m+3-m)•$\frac{{m}^{2}-3+m}{m}$
=3×$\frac{m+3-3+m}{m}$
=3×2
=6.
点评 本题考查了一元二次方程的解:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.

练习册系列答案
相关题目
8.某校调查在校七年级学生的身高,在七年级学生中随机抽取35名学生进行了调查,具体数据如下:
可估算出该校七年级学生的平均身高为160.8cm.
| 身高(cm) | 158 | 159 | 160 | 161 | 162 | 163 |
| 人数(个) | 6 | 3 | 6 | 6 | 5 | 9 |
9. 实数a、b在数轴上的位置如图所示,则下列各式表示正确的是( )
实数a、b在数轴上的位置如图所示,则下列各式表示正确的是( )
 实数a、b在数轴上的位置如图所示,则下列各式表示正确的是( )
实数a、b在数轴上的位置如图所示,则下列各式表示正确的是( )| A. | b-a<0 | B. | 1-a>0 | C. | b-1>0 | D. | -1-b<0 |
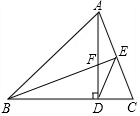 如图,在Rt△BDF中,∠BDF=90°,把△BDF绕点D顺时针旋转90°,使点B和点F分别落在DF、BD的延长线上的点A和点C处,延长BF与AC交于点E,连接AB、DE.
如图,在Rt△BDF中,∠BDF=90°,把△BDF绕点D顺时针旋转90°,使点B和点F分别落在DF、BD的延长线上的点A和点C处,延长BF与AC交于点E,连接AB、DE.