题目内容
已知：a+b=8，ab=7，求a-b和a2-b2的值．
考点：完全平方公式,平方差公式
专题：计算题
分析：将a+b=8两边平方，利用完全平方公式展开，把ab的值代入求出a2+b2的值，再利用完全平方公式求出a-b的值，进而确定出a2-b2的值．
解答：解：将a+b=8两边平方得：（a+b）2=a2+b2+2ab=64，
把ab=7代入得：a2+b2=50，
∴（a-b）2=a2+b2-2ab=50-14=36，
开方得：a-b=6或a-b=-6，
当a-b=6时，a2-b2=（a+b）（a-b）=48；
当a-b=-6时，a2-b2=（a+b）（a-b）=-48．
把ab=7代入得：a2+b2=50，
∴（a-b）2=a2+b2-2ab=50-14=36，
开方得：a-b=6或a-b=-6，
当a-b=6时，a2-b2=（a+b）（a-b）=48；
当a-b=-6时，a2-b2=（a+b）（a-b）=-48．
点评：此题考查了完全平方公式，以及平方差公式，熟练掌握公式是解本题的关键．
练习册系列答案
相关题目
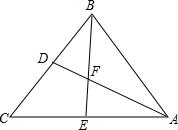如图，△ABC的中线为AD，BE相交于点F，若△ABC的面积是45，求四边形DCEF的面积．
一时装表演会预定票价每张100元，会场容纳观众不超过1000人，利润y（百元）关于观众人数x（百人）之间的函数关系如图：