题目内容
直线y1=2x+3和直线y2=-2x-1分别交y轴于点A、B,两直线交于点C(-1,n).
(1)求n的值;
(2)求△ABC的面积;
(3)请根据图象直接写出直线y1>y2时自变量的取值范围.
(1)求n的值;
(2)求△ABC的面积;
(3)请根据图象直接写出直线y1>y2时自变量的取值范围.
考点:两条直线相交或平行问题
专题:
分析:(1)把点C的坐标代入y1=2x+3来求n的值即可;
(2)根据点A、B的坐标求得AB的长度;由点C的横坐标的绝对值即为该三角形的高;
(3)根据图示直接写出答案.
(2)根据点A、B的坐标求得AB的长度;由点C的横坐标的绝对值即为该三角形的高;
(3)根据图示直接写出答案.
解答: 解:(1)∵点C(-1,n)在直线y1=2x+3上,
解:(1)∵点C(-1,n)在直线y1=2x+3上,
∴n=2×(-1)+3=1.即n=1;
(2)∵y1=2x+3与y轴的交点A(0,3),直线y2=-2x-1与y轴的交点B(0,-1).
∴AB=4.
又C(-1,1).
∴△ABC的面积=
×4×1=2;
(3)根据图示知,当直线y1>y2时,x>-1.
 解:(1)∵点C(-1,n)在直线y1=2x+3上,
解:(1)∵点C(-1,n)在直线y1=2x+3上,∴n=2×(-1)+3=1.即n=1;
(2)∵y1=2x+3与y轴的交点A(0,3),直线y2=-2x-1与y轴的交点B(0,-1).
∴AB=4.
又C(-1,1).
∴△ABC的面积=
| 1 |
| 2 |
(3)根据图示知,当直线y1>y2时,x>-1.
点评:本题考查了两条直线相交或平行问题.注意“数学结合”数学思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知△ABC中,
如图,已知△ABC中,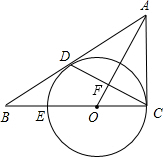 如图,△ABC中,∠ACB=90°,D是边AB上的一点,E是BC上的一点,以EC为直径的⊙O经过点D,OA⊥CD于点F.
如图,△ABC中,∠ACB=90°,D是边AB上的一点,E是BC上的一点,以EC为直径的⊙O经过点D,OA⊥CD于点F.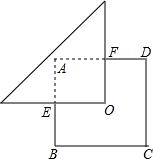 如图,O是边长为a的正方形ABCD的中心,将一块腰长足够长的等腰直角三角形纸板的直角顶点放在O处,并将纸板绕O点旋转.问正方形被纸板覆盖部分的面积是否发生变化.请说明理由.
如图,O是边长为a的正方形ABCD的中心,将一块腰长足够长的等腰直角三角形纸板的直角顶点放在O处,并将纸板绕O点旋转.问正方形被纸板覆盖部分的面积是否发生变化.请说明理由.