题目内容
如图,AB是⊙O的直径,AM、BN分别切⊙O于点A、B,CD交AM,BN于点D、C,DO平分∠ADC.
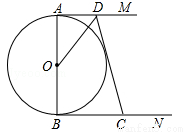
(1)求证:CD是⊙O的切线;
(2)若AD=4,BC=9,求⊙O的半径R.
(1)证明见试题解析;(2)6.
【解析】
试题分析:(1)过O点作OE⊥CD于点E,通过角平分线的性质得出OE=OA即可证得结论;
(2)过点D作DF⊥BC于点F,根据切线的性质可得出DC的长度,在Rt△DFC中利用勾股定理可得出DF的长,从而可得出半径.
试题解析:(1)过O点作OE⊥CD于点E,∵AM切⊙O于点A,∴OA⊥AD,又∵DO平分∠ADC,∴OE=OA,∵OA为⊙O的半径,∴OE是⊙O的半径,且OE⊥DC,∴CD是⊙O的切线;
(2)过点D作DF⊥BC于点F,∵AM,BN分别切⊙O于点A,B,∴AB⊥AD,AB⊥BC,∴四边形ABFD是矩形,∴AD=BF,AB=DF,又∵AD=4,BC=9,∴FC=9﹣4=5,∵AM,BN,DC分别切⊙O于点A,B,E,∴DA=DE,CB=CE,∴DC=AD+BC=4+9=13,在Rt△DFC中, ,∴DF=
,∴DF= ,∴AB=12,∴⊙O的半径R是6.
,∴AB=12,∴⊙O的半径R是6.

考点:1.切线的判定与性质;2.全等三角形的判定与性质;3.勾股定理;4.圆周角定理.

练习册系列答案
相关题目
 ∠B都是锐角,且 sin A=
∠B都是锐角,且 sin A= ,cos B=
,cos B= ,则△ABC三个角的大小关系是( )
,则△ABC三个角的大小关系是( )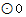 的直径,点D在
的直径,点D在
 -5x+6=0的两根,两圆的圆心距为1,则两圆的位置关系是( )
-5x+6=0的两根,两圆的圆心距为1,则两圆的位置关系是( ) (1≤x≤30,且x为整数);又知前20天的销售价格Q1(元/件)与销售时间x(天)之间有如下关系:
(1≤x≤30,且x为整数);又知前20天的销售价格Q1(元/件)与销售时间x(天)之间有如下关系: (1≤x≤20,且x为整数),后10天的销售价格Q2(元/件)与销售时间x(天)之间有如下关系:Q2=45(21≤x≤30,且x为整数).
(1≤x≤20,且x为整数),后10天的销售价格Q2(元/件)与销售时间x(天)之间有如下关系:Q2=45(21≤x≤30,且x为整数). =
= 的图象向左平移1个单位,再向上平移1个单位,所得图象对应的函数的解析式是( )
的图象向左平移1个单位,再向上平移1个单位,所得图象对应的函数的解析式是( ) B.
B. C.
C. D.
D.
 (
( )的图象如图,关于该二次函数,下列说法错误的是( )
)的图象如图,关于该二次函数,下列说法错误的是( )

 ,y随x的增大而减小 D.当
,y随x的增大而减小 D.当 时,
时,
