题目内容
(7分)关于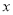 的方程为
的方程为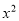 +(m+2)x+2m-1=0.
+(m+2)x+2m-1=0.
(1)、证明:方程有两个不相等的实数根.
(2)、是否存在实数m,使方程的两个实数根互为相反数?若存在,求出m的值及两个实数根;若不存在,请说明理由.
(1)、见解析;(2)、m=-2,x=± .
.
【解析】
试题分析:(1)、根据韦达定理来进行说明;(2)、两根互为相反数则说明两个之和为0,然后求出m的值,将m的值代入方程求出方程的解.
试题解析:(1)证明:△= -4(2m-1)=
-4(2m-1)= -4m+8=
-4m+8= +4 ∵
+4 ∵ ≥0
≥0
∴ +4>0 ∴方程有两个不相等的实数根.
+4>0 ∴方程有两个不相等的实数根.
(2)、存在实数m,使方程的两个实数根互为相反数. 由题知: =-(m+2)=0
=-(m+2)=0
解得:m=-2 将m=-2代入方程可得: -5=0,解得:x=±
-5=0,解得:x=±
∴m的值为-2,方程的根为± .
.
考点:根的判别式、韦达定理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,则tanB等于( )
,则tanB等于( ) B.
B. C
C .
.
 D.
D.

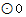 的直径,点D在
的直径,点D在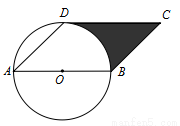
 +
+ )(2
)(2 -5x+6=0的两根,两圆的圆心距为1,则两圆的位置关系是( )
-5x+6=0的两根,两圆的圆心距为1,则两圆的位置关系是( )