题目内容
 如图,点A的坐标为(2,0),以点A为圆心,1厘米长度为半径画圆,点P是第一象限⊙A上的一个动点,则∠POA的最大度数为
如图,点A的坐标为(2,0),以点A为圆心,1厘米长度为半径画圆,点P是第一象限⊙A上的一个动点,则∠POA的最大度数为考点:切线的性质,坐标与图形性质
专题:
分析:当OP与圆A相切时,∠POA的度数最大,此时连接AP,则AP⊥OP,利用三角函数的知识可确定∠POA的度数.
解答:解:当OP与圆A相切时,∠POA的度数最大,
如图所示:

连接AP,则AP⊥OP,
∵圆A的半径为1,点A的坐标为(2,0),
∴AP=1,OA=2,
∵sin∠POA=
=
,
∴∠POA=30°.
即∠POA的最大度数为30°.
故答案为:30°.
如图所示:

连接AP,则AP⊥OP,
∵圆A的半径为1,点A的坐标为(2,0),
∴AP=1,OA=2,
∵sin∠POA=
| AP |
| OA |
| 1 |
| 2 |
∴∠POA=30°.
即∠POA的最大度数为30°.
故答案为:30°.
点评:本题考查了切线的性质,首先判断出当OP与圆A相切时,∠POA的度数最大,是解答本题的关键,难度一般.

练习册系列答案
相关题目
江苏大学最新研究,家蚕二分浓核病毒直径长度只有22纳米左右,必须通过40万倍电镜观察,22纳米用科学记数法应表示为( )
| A、22×10-9米 |
| B、2.2×10-8米 |
| C、22×10-8米 |
| D、2.2×10-9米 |
如图,已知AB=AC,AB∥EF,若∠CDE=60°,则∠C等于( )

| A、15° | B、30° |
| C、45° | D、60° |
计算(-4a)2的结果是( )
| A、8a2 |
| B、-8a2 |
| C、-16a2 |
| D、16a2 |
下列方程中有两个相等的实数根的是( )
| A、x2=1 |
| B、(x+1)2=0 |
| C、x2+1=0 |
| D、2(x+1)=0 |
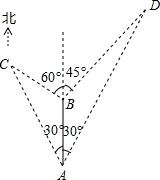 如图,在一次数学应用活动中,小明沿一条南北公路向北行走,在A处,他测得左边建筑C在北偏西30°方向,右边建筑D在北偏东30°方向;从A出向北40米行至B处,他又测得左边建筑物C在北偏西60°方向,右边建筑物D在北偏东45°方向.请根据以上数据求两建筑物C、D到这条南北公路的距离.
如图,在一次数学应用活动中,小明沿一条南北公路向北行走,在A处,他测得左边建筑C在北偏西30°方向,右边建筑D在北偏东30°方向;从A出向北40米行至B处,他又测得左边建筑物C在北偏西60°方向,右边建筑物D在北偏东45°方向.请根据以上数据求两建筑物C、D到这条南北公路的距离. 如图,已知正方形ABCD中,E、F分别在AB、BC上,△DEF为正三角形,则∠AED=
如图,已知正方形ABCD中,E、F分别在AB、BC上,△DEF为正三角形,则∠AED=