题目内容
 如图,已知正方形ABCD中,E、F分别在AB、BC上,△DEF为正三角形,则∠AED=
如图,已知正方形ABCD中,E、F分别在AB、BC上,△DEF为正三角形,则∠AED=考点:正方形的性质,全等三角形的判定与性质,等边三角形的性质
专题:
分析:根据正方形的性质和等边三角形的性质可证△DAE≌△DCF,根据全等三角形的性质可得AE=CF,从而得到△EBF是等腰直角三角形,再根据等腰直角三角形的性质和平角的定义即可求解.
解答:解:∵△DEF为正三角形,
∴DE=DF,∠DEF=60°,
∵四边形ABCD是正方形,
∴AD=CD=AB=BC,∠A=∠C=90°,
在Rt△DAE与Rt△DCF中,
,
∴Rt△DAE≌Rt△DCF(HL),
∴AE=CF,
∴BE=BF,
∴△EBF是等腰直角三角形,
∴∠BEF=45°,
∴∠AED=180°-60°-45°=75°.
故答案为:75.
∴DE=DF,∠DEF=60°,
∵四边形ABCD是正方形,
∴AD=CD=AB=BC,∠A=∠C=90°,
在Rt△DAE与Rt△DCF中,
|
∴Rt△DAE≌Rt△DCF(HL),
∴AE=CF,
∴BE=BF,
∴△EBF是等腰直角三角形,
∴∠BEF=45°,
∴∠AED=180°-60°-45°=75°.
故答案为:75.
点评:考查了正方形的性质和等边三角形的性质,全等三角形的判定与性质,等腰直角三角形的性质,解题的关键是得到△EBF是等腰直角三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
要反映杭州市一天内气温的变化情况,比较适宜采用的是( )
| A、折线统计图 |
| B、条形统计图 |
| C、扇形统计图 |
| D、频数分布统计图 |
 如图,由两块长方体叠成的几何体,其主视图是( )
如图,由两块长方体叠成的几何体,其主视图是( )A、 |
B、 |
C、 |
D、 |
 有5张正面分别标有数字-1,0,1,2,3的不透明卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后[从中任取一张,将该卡片上的数字记为m,则使关于x的二次函数y=x2-2mx+1的图象与端点为A(-1,1)和B(4,3)的线段(如图)只有一个交点的概率为
有5张正面分别标有数字-1,0,1,2,3的不透明卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后[从中任取一张,将该卡片上的数字记为m,则使关于x的二次函数y=x2-2mx+1的图象与端点为A(-1,1)和B(4,3)的线段(如图)只有一个交点的概率为 如图,点A的坐标为(2,0),以点A为圆心,1厘米长度为半径画圆,点P是第一象限⊙A上的一个动点,则∠POA的最大度数为
如图,点A的坐标为(2,0),以点A为圆心,1厘米长度为半径画圆,点P是第一象限⊙A上的一个动点,则∠POA的最大度数为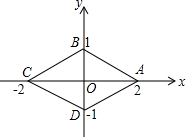 如图,菱形ABCD的顶点分别在x轴或y轴上,物体甲和物体乙分别由点A(2,0)同时出发,沿菱形ABCD的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以3个单位/秒匀速运动,则两个物体运动后的第2013次相遇地点的坐标是
如图,菱形ABCD的顶点分别在x轴或y轴上,物体甲和物体乙分别由点A(2,0)同时出发,沿菱形ABCD的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以3个单位/秒匀速运动,则两个物体运动后的第2013次相遇地点的坐标是