题目内容
下列方程中有两个相等的实数根的是( )
| A、x2=1 |
| B、(x+1)2=0 |
| C、x2+1=0 |
| D、2(x+1)=0 |
考点:根的判别式
专题:计算题
分析:各选项中的方程整理为一般形式,找出方程中的a,b及c的值,计算出根的判别式的值,根的判别式值为0即满足题意.
解答:解:A、方程整理得:x2-1=0,
这里a=1,b=0,c=-1,
∵△=b2-4ac=4>0,
∴方程有两个不相等的实数根,本选项不合题意;
B、方程整理得:x2+2x+1=0,
这里a=1,b=2,c=1,
∵△=b2-4ac=0,
∴方程有两个相等的实数根,本选项符合题意;
C、这里a=1,b=0,c=1,
∵△=b2-4ac=-4<0,
∴方程没有实数根,本选项不合题意;
D、2x+2=0为一元一次方程,只有一个解,本选项不合题意,
故选B
这里a=1,b=0,c=-1,
∵△=b2-4ac=4>0,
∴方程有两个不相等的实数根,本选项不合题意;
B、方程整理得:x2+2x+1=0,
这里a=1,b=2,c=1,
∵△=b2-4ac=0,
∴方程有两个相等的实数根,本选项符合题意;
C、这里a=1,b=0,c=1,
∵△=b2-4ac=-4<0,
∴方程没有实数根,本选项不合题意;
D、2x+2=0为一元一次方程,只有一个解,本选项不合题意,
故选B
点评:此题考查了根的判别式,根的判别式的值大于0,方程有两个不相等的实数根;根的判别式的值等于0,方程有两个相等的实数根;根的判别式的值小于0,方程没有实数根.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知
+
=
(a≠b),则
-
的值为( )
| 1 |
| a |
| 1 |
| b |
| 3 |
| a |
| b(a-b) |
| b |
| a(a-b) |
A、
| ||
B、2
| ||
| C、2 | ||
| D、1 |
 如图,由两块长方体叠成的几何体,其主视图是( )
如图,由两块长方体叠成的几何体,其主视图是( )A、 |
B、 |
C、 |
D、 |
 如图,点A的坐标为(2,0),以点A为圆心,1厘米长度为半径画圆,点P是第一象限⊙A上的一个动点,则∠POA的最大度数为
如图,点A的坐标为(2,0),以点A为圆心,1厘米长度为半径画圆,点P是第一象限⊙A上的一个动点,则∠POA的最大度数为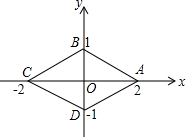 如图,菱形ABCD的顶点分别在x轴或y轴上,物体甲和物体乙分别由点A(2,0)同时出发,沿菱形ABCD的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以3个单位/秒匀速运动,则两个物体运动后的第2013次相遇地点的坐标是
如图,菱形ABCD的顶点分别在x轴或y轴上,物体甲和物体乙分别由点A(2,0)同时出发,沿菱形ABCD的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以3个单位/秒匀速运动,则两个物体运动后的第2013次相遇地点的坐标是 小明利用测角仪测量学校内一棵大树的高度,已知他离树的水平距离BC为12m,测角仪的高度CD为1.4m,测到树顶A的仰角为50°,求树的高度AB.
小明利用测角仪测量学校内一棵大树的高度,已知他离树的水平距离BC为12m,测角仪的高度CD为1.4m,测到树顶A的仰角为50°,求树的高度AB.