题目内容
19．已知（x-2）5=ax5+bx4+cx3+dx2+ex+f，则16b+4d+f=-512．分析 分别将x=2和x=-2代入代数式，然后将两式相减可求得代数式的值．
解答 解：将x=2代入得：32a+16b+8c+4d+2e+f=0①．
将x=-2代入得：-32a+16b-8c+4d-2e+f=-1024②
①+②得：2（16b+4d+f）=-1024．
∴16b+4d+f=-512．
故答案为：-512．
点评 本题主要考查的是求代数式的值，利用特殊值法求得32a+16b+8c+4d+2e+f=0、-32a+16b-8c+4d-2e+f=-1024是解题的关键．
练习册系列答案
相关题目
7．若代数式-a2+2a+1的值为-4，则代数式$\frac{1}{4}$a2-$\frac{1}{2}$a+5的值为（ ）
| A． | $\frac{25}{4}$ | B． | -$\frac{15}{4}$ | C． | $\frac{15}{4}$ | D． | 1 |
14．下列方程是一元一次方程的是（ ）
| A． | y2+2y=y（y-2）-3 | B． | $\frac{3x-4}{2}+5=\frac{3}{2}x+3$ | C． | $\frac{2}{x}+3x=7+\frac{2}{x}$ | D． | 3x-8y=13 |
11．
如图，BC⊥AE于点C，CD∥AB，∠1=55°，则∠B等于（ ）
如图，BC⊥AE于点C，CD∥AB，∠1=55°，则∠B等于（ ）| A． | 35° | B． | 45° | C． | 55° | D． | 65° |
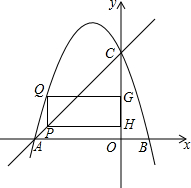如图，在平面直角坐标系中，抛物线y=ax2+bx+3与x轴交于点A（-3，0）、B（1，0），与y轴交于点C．点P为线段AC上一点（不与点A、C重合），PH⊥y轴于点H，PQ∥y轴交抛物线于点Q，QG⊥y轴于点G．设点P的横坐标为m．