题目内容
15.(1)如图1,已知AB∥A'B',∠B=∠B',请判断BC与B'C'是否平行,并说明理由.(2)如图2所示,若将周长为16 cm的△ABC沿边AC向右平移3 cm得到△A'B'C',求四边形ABB'C'的周长.(简要说明理由).
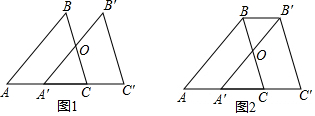
分析 (1)根据AB∥A'B',得到∠A=∠B′A′C′,根据相似三角形的性质得到∠ACB=∠C′由平行线的判定即可得到结论;
(2)由平移的性质得到BC=B′C′,BB′=CC′=3cm,即可得到结论.
解答 解:(1)BC与B'C'平行,
理由:∵AB∥A'B',
∴∠A=∠B′A′C′,
∵∠B=∠B',
∴△ABC∽△A′B′C′,
∴∠ACB=∠C′
∴BC∥B'C';
(2)∵将△ABC沿边AC向右平移3 cm得到△A'B'C',
∴BC=B′C′,BB′=CC′=3cm,
∴四边形ABB'C'的周长=AB+AC+B′C′+B′B+CC′=AB+AC+BC+6,
∵△ABC的周长为16 cm,
∴四边形ABB'C'的周长=22cm.
点评 本题考查了平移的性质,平行线的判定和性质,熟练掌握平移的性质是解题的关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
5.若点M(a-4,3a-6)在x轴上,则点M的坐标为( )
| A. | (0,6) | B. | (2,0) | C. | (-2,0) | D. | (0,-2) |
6.若|x-3|与|2y-3|互为相反数,则xy+x-y的值是( )
| A. | 6 | B. | -6 | C. | -$\frac{3}{2}$ | D. | $\frac{3}{2}$ |
3.在一个不透明的口袋中装有4个红球和若干个白球,它们除颜色外其他完全相同.通过多次摸球试验后发现,摸到红球的频率稳定在25%附近,则口袋中白球可能有( )
| A. | 13个 | B. | 12个 | C. | 16个 | D. | 15个 |
4.某天的最高气温是5℃,最低气温是-4℃,则这一天气温的温差是( )
| A. | 1℃ | B. | -1℃ | C. | 9℃ | D. | -9℃ |
5.某体校要从四名射击选手中选拔一名参加体育运动会,选拔赛中每名选手连续射靶10次,他们各自的平均成绩及其方差s2如表所示,如果要选出一名成绩高,且发挥稳定的选手参赛,则应选择的选手是乙.
| 甲 | 乙 | 丙 | 丁 | |
| $\overline{x}$(环) | 8.4 | 8.6 | 8.6 | 7.6 |
| S2 | 0.74 | 0.56 | 0.94 | 1.92 |
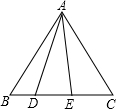 在等边三角形ABC中,点D在BC上,且BD:DC=1:4,连接DA,作∠DAE,满足∠DAE=30°,则tan∠BAE的值是$\frac{\sqrt{3}}{2}$.
在等边三角形ABC中,点D在BC上,且BD:DC=1:4,连接DA,作∠DAE,满足∠DAE=30°,则tan∠BAE的值是$\frac{\sqrt{3}}{2}$.