题目内容
6. 如图,△ABC中,∠C=90°,AC=BC,AD是∠BAC的角平分线,DE⊥AB于E,若AB=10cm,则△DBE的周长等于( )
如图,△ABC中,∠C=90°,AC=BC,AD是∠BAC的角平分线,DE⊥AB于E,若AB=10cm,则△DBE的周长等于( )| A. | 10cm | B. | 8cm | C. | 6cm | D. | 9cm |
分析 根据角平分线的性质得:CD=DE,利用HL证明Rt△ACD≌Rt△AED,得AC=AE,所以BC=AE,代入△DBE的周长可得结果.
解答 解:∵AD是∠BAC的角平分线,∠C=90°,DE⊥AB,
∴CD=DE,
∵AD=AD,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE,
∵AC=BC,
∴AC=BC=AE,
∴△DBE的周长=DE+BE+BD=CD+BD+BE=BC+BE=AE+BE=AB=10cm,
故选A.
点评 本题考查了等腰直角三角形和角平分线的性质,以及全等三角形的性质和判定,在求三角形周长时,如果所对应的边不能依次求出,可以利用整体的思想,将所求周长的三角形各边利用相等关系转化为其它边,利用已知条件得出结论.

练习册系列答案
相关题目
16.如图,直角三角形纸片ABC中AB=3,AC=4,D为斜边BC中点,第1次将纸片折叠,使点A与点D重合,折痕与AD交于点P1;设P1D的中点为D1,第2次将纸片折叠,使点A与点D1重合,折痕与AD交于P2;设P2D1的中点为D2,第3次将纸片折叠,使点A与点D2重合,折痕与AD交于点P3;设Pn-1Dn-2的中点为Dn-1,第n次将纸片折叠,使点A与点Dn-1重合,折痕与AD交于点Pn(n>2),则AP6的长为( )


| A. | $\frac{{3}^{5}}{5×{2}^{9}}$ | B. | $\frac{5×{3}^{5}}{{2}^{12}}$ | C. | $\frac{5×{3}^{6}}{{2}^{14}}$ | D. | $\frac{{3}^{7}}{5×{2}^{11}}$ |
 两棵树在一盏路灯下的影子如图所示
两棵树在一盏路灯下的影子如图所示 如图,△ABC内接于⊙O,⊙O的半径为6,连接OB、OC.若∠BAC与∠BOC互补,求弦BC的长.
如图,△ABC内接于⊙O,⊙O的半径为6,连接OB、OC.若∠BAC与∠BOC互补,求弦BC的长.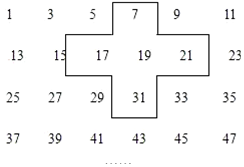 实践与探索:将连续的奇数1,3,5,7…排列成如图的数表用十字框框出5个数(如图)
实践与探索:将连续的奇数1,3,5,7…排列成如图的数表用十字框框出5个数(如图) 如图,给正五边形的顶点依次编号为1,2,3,4,5.若从某一顶点开始,沿正五边形的边顺时针方向行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”.如:小宇在编号为2的顶点上时,那么他应走2个边长,即从2→3→4为第一次“移位”,这时他到达编号为4的顶点;然后从4→3为第二次“移位”.若小宇从编号为3的顶点开始,第2017次“移位”后,则他所处顶点的编号是1.
如图,给正五边形的顶点依次编号为1,2,3,4,5.若从某一顶点开始,沿正五边形的边顺时针方向行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”.如:小宇在编号为2的顶点上时,那么他应走2个边长,即从2→3→4为第一次“移位”,这时他到达编号为4的顶点;然后从4→3为第二次“移位”.若小宇从编号为3的顶点开始,第2017次“移位”后,则他所处顶点的编号是1.