题目内容
16. 两棵树在一盏路灯下的影子如图所示
两棵树在一盏路灯下的影子如图所示(1)确定该路灯灯泡的位置(用点P表示).
(2)画出表示婷婷的影长的线段(用线段AB表示).
(3)若小树高为2m,影长为4m;婷婷高1.5rn,影长为4.5米,且婷婷距离小树10米,试求出路灯灯泡的高度.
分析 (1)根据中心投影的特点可知,连接物体和它影子的顶端所形成的直线必定经过点光源.所以分别把两棵树的顶端和影子的顶端连接并延长可交于一点,即点光源的位置;
(2)连接PC并延长交QA的延长线与点B,即可得;
(3)由DF∥PQ得△DEF∽△QEP,根据相似三角形的性质有$\frac{DF}{PQ}=\frac{DE}{QE}$,即$\frac{2}{PQ}=\frac{4}{QD+4}$ ①,同理可得$\frac{CA}{PQ}=\frac{AB}{QB}$,即$\frac{1.5}{PQ}=\frac{4.5}{QD+10+4.5}$ ②,联立①②可得PQ.
解答 解:(1)如图,点P即为灯泡所在位置;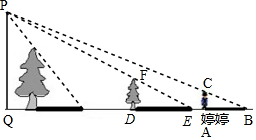
(2)如图,线段AB即为婷婷的影长;
(3)由题意知,DF=2,DE=4,DA=10,AC=1.5,AB=4.5,
∵DF∥PQ,
∴△DEF∽△QEP,
∴$\frac{DF}{PQ}=\frac{DE}{QE}$,即$\frac{2}{PQ}=\frac{4}{QD+4}$ ①,
∵CA∥PQ,
∴△CAB∽△PQB,
∴$\frac{CA}{PQ}=\frac{AB}{QB}$,即$\frac{1.5}{PQ}=\frac{4.5}{QD+10+4.5}$ ②,
由①②可得PQ=10.5,
答:路灯灯泡的高度为10.5m.
点评 本题考查了中心投影和相似三角形的应用:利用影长测量物体的高度,通常利用相似三角形的性质即相似三角形的对应边的比相等和“在同一时刻物高与影长的比相等”的原理解决.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6. 如图,△ABC中,∠C=90°,AC=BC,AD是∠BAC的角平分线,DE⊥AB于E,若AB=10cm,则△DBE的周长等于( )
如图,△ABC中,∠C=90°,AC=BC,AD是∠BAC的角平分线,DE⊥AB于E,若AB=10cm,则△DBE的周长等于( )
 如图,△ABC中,∠C=90°,AC=BC,AD是∠BAC的角平分线,DE⊥AB于E,若AB=10cm,则△DBE的周长等于( )
如图,△ABC中,∠C=90°,AC=BC,AD是∠BAC的角平分线,DE⊥AB于E,若AB=10cm,则△DBE的周长等于( )| A. | 10cm | B. | 8cm | C. | 6cm | D. | 9cm |
 如图,A、B分别为y=x2图象上的两点,且AB⊥y轴,AB=6,
如图,A、B分别为y=x2图象上的两点,且AB⊥y轴,AB=6, 如图所示是一个长方形.
如图所示是一个长方形.