题目内容
8.下列各组线段中,能构成直角三角形的是( )| A. | 2cm,3cm,4cm | B. | 1cm,1cm,$\sqrt{2}$cm | C. | 5cm,12cm,14cm | D. | $\sqrt{3}$cm,$\sqrt{4}$cm,$\sqrt{5}$cm |
分析 由勾股定理的逆定理,只要验证两小边的平方和等于最长边的平方即可.
解答 解:A、22+32≠42,故不是直角三角形,故此选不符合题意;
B、12+12=2=($\sqrt{2}$)2,故是直角三角形,故此选项符合题意;
C、22+122=≠142,故不是直角三角形,故此选项不符合题意;
D、($\sqrt{3}$)2+($\sqrt{4}$)2≠($\sqrt{5}$)2,故不是直角三角形,故此选项不符合题意.
故选B.
点评 本题考查勾股定理的逆定理,判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.

练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
3.完成下列填空:$\frac{3x}{1.2}$-$\frac{1.5-x}{2}$=0.6,解:化简,得:2.5x-( )=0.6.括号内填入的应该是( )
| A. | $\frac{15-10x}{20}$ | B. | 0.75-0.5x | C. | $\frac{15-x}{2}$ | D. | 0.75+0.5x |
20.一种商品原价200元,由于市场情况不好,经过连续两次降价m%后售价为148元,则下面所列方程中正确的是( )
| A. | 200(1+m%)2=148 | B. | 200(1-m%)2=148 | C. | 200(1-2m%)2=148 | D. | 200[1-(m%)2]=148 |
 如图,从A地到B地的公路需经过C地,图中AC=10千米,∠CAB=25°,∠CBA=37°,因城市规划的需要,将在A、B两地之间修建一条笔直的公路.求改直的公路AB的长.
如图,从A地到B地的公路需经过C地,图中AC=10千米,∠CAB=25°,∠CBA=37°,因城市规划的需要,将在A、B两地之间修建一条笔直的公路.求改直的公路AB的长.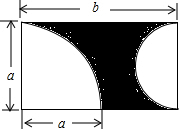 如图,用整式表示图中阴影部分的面积,并计算当a=4cm,b=8cm时的阴影部分的面积(结果保留π)
如图,用整式表示图中阴影部分的面积,并计算当a=4cm,b=8cm时的阴影部分的面积(结果保留π) 如图,在Rt△ABC中,∠C=90°,AB=6cm,AD平分∠BAC,交BC于点D,CD=3cm,则△ABD的面积是多少?
如图,在Rt△ABC中,∠C=90°,AB=6cm,AD平分∠BAC,交BC于点D,CD=3cm,则△ABD的面积是多少?