题目内容
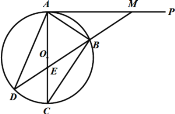
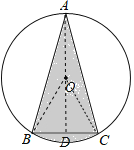
【题目】如图，⊙O中，AB＝AC，∠ACB＝75°，BC＝1，则阴影部分的面积是（ ）
A.1+
πB.
πC.
πD.1+
π
【答案】B
【解析】
连接OB、OC，先利用同弧所对的圆周角等于所对的圆心角的一半，求出扇形的圆心角为60度，即可求出半径的长1，利用三角形和扇形的面积公式即可求解；
解：作OD⊥BC，则BD=CD，连接OA，OB，OC，
∴OD是BC的垂直平分线 ∴
，
∴AB=AC， ∴A在BC的垂直平分线上，
∴A、O、D共线，
∵∠ACB=75°，AB=AC， ∴∠ABC=∠ACB=75°，
∴∠BAC=30°， ∴∠BOC=60°，
∵OB=OC， ∴△BOC是等边三角形，
∴OA=OB=OC=BC=1，
∵AD⊥BC，AB=AC， ∴BD=CD，
∴OD=
=
，
∴AD=
，
∴
，
，
∴
阴影=
+扇形BOC－
=
，
故选：B．
练习册系列答案
相关题目
【题目】在2019年端午节前夕，某商场投入13800元资金购进甲、乙两种商品共500件，两种商品的成本价和销售价如下表所示：
商品 单价（元/件） | 成本价 | 销售价 |
甲 | 24 | 36 |
乙 | 33 | 48 |
（1）该商场购进两种商品各多少件？
（2）这批商品全部销售完后，该商场共获利多少元？
