题目内容
18．已知：⊙O中，弦AB垂直于直径CD，垂足为P，AB=12，CP=2，则⊙O的直径为20．分析 连接OA，设圆的半径为R，根据垂径定理和勾股定理列出关于R的方程，解方程得到答案．
解答 解：
连接OA，
设圆的半径为R，
∵弦AB垂直于直径CD，垂足为P，AB=12，
∴AP=6，
由勾股定理得，OA2=OP2+AP2，
即R2=62+（R-2）2，
解得R=10．
则⊙O的直径为20．
故答案为：20．
点评 本题考查的是垂径定理和勾股定理的应用，掌握垂直于弦的直径平分这条弦，并且平分弦所对的两条弧是解题的关键．注意方程思想在解题中的作用．
练习册系列答案
阅读快车系列答案
相关题目
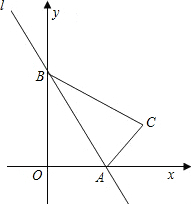如图，直线l：y=-$\sqrt{3}$x+$\sqrt{3}$与x轴，y轴分别相交于点A，B，△AOB与△ACB关于直线L对称．
一条长为40m的篱笆一面靠墙围成长方形空地，中间隔开，已知墙宽10m，则长方形空地的长y关于宽x的函数关系式是y=40-4x，自变量的范围是0＜x＜10．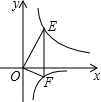
如图，直线EF∥y轴，分别交双曲线y=$\frac{8}{x}$（x＞0和y=-$\frac{2}{x}$（x＞0）的图象于E、F，且OE⊥OF，则EF=5．