题目内容
在半径为1的⊙O中内接有锐角△ABC,H是△ABC的垂心,角平分线AL垂直于OH,则BC= .
考点:三角形的五心
专题:
分析:设AL与⊙O交于点D,与OH交于点N,连接OD,交BC于点M,连接CO并延长交⊙O于点G,连接GA、GB、AO,易证四边形AGBH是平行四边形,则有BG=AH.易证OD∥AE,结合OA=OD可证到∠OAN=∠HAN,从而可证到△ANO≌△ANH,则有AO=AH,从而得到BG=1,然后在Rt△GBC中运用勾股定理即可求出BC的值.
解答:解:设AL与⊙O交于点D,与OH交于点N,连接OD,交BC于点M,连接CO并延长交⊙O于点G,连接GA、GB、AO,如图所示,
∵CG是⊙O的直径,∴∠CBG=∠CAG=90°,
∴BG⊥BC,AG⊥AC.
∵H为△ABC的垂心,
∴AE⊥BC,BF⊥AC,
∴AE∥BG,AG∥BF,
∴四边形AGBH是平行四边形,
∴BG=AH.
∵AL平分∠BAC,∴∠BAD=∠CAD,
∴
=
,
根据垂径定理的推论可得:OD⊥BC.
∵AE⊥BC,∴OD∥AE,
∴∠ODA=∠EAD.
∵OA=OD,∴∠ODA=∠OAD,
∴∠OAD=∠EAD.
∵AL垂直于OH,
∴∠ANO=∠ANH=90°.
在△ANO和△ANH中,
,
∴△ANO≌△ANH(ASA),
∴AO=AH,
∴BG=AH=AO=1.
在Rt△GBC中,
∵BG=1,GC=2,
∴BC=
=
.
故答案为:
.
∵CG是⊙O的直径,∴∠CBG=∠CAG=90°,
∴BG⊥BC,AG⊥AC.
∵H为△ABC的垂心,
∴AE⊥BC,BF⊥AC,
∴AE∥BG,AG∥BF,
∴四边形AGBH是平行四边形,
∴BG=AH.

∵AL平分∠BAC,∴∠BAD=∠CAD,
∴
 |
| BD |
 |
| CD |
根据垂径定理的推论可得:OD⊥BC.
∵AE⊥BC,∴OD∥AE,
∴∠ODA=∠EAD.
∵OA=OD,∴∠ODA=∠OAD,
∴∠OAD=∠EAD.
∵AL垂直于OH,
∴∠ANO=∠ANH=90°.
在△ANO和△ANH中,
|
∴△ANO≌△ANH(ASA),
∴AO=AH,
∴BG=AH=AO=1.
在Rt△GBC中,
∵BG=1,GC=2,
∴BC=
| GC2-BG2 |
| 3 |
故答案为:
| 3 |
点评:本题主要考查了三角形的外心、垂心、平行四边形的判定与性质、垂径定理的推论、全等三角形的判定与性质、勾股定理等知识,证到四边形AGBH是平行四边形及△ANO≌△ANH是解决本题的关键.

练习册系列答案
相关题目
下列判断中正确的是( )
A、若
| ||
| B、若1+2x=7,则x=3 | ||
| C、若4x=2,则x=2 | ||
| D、若2x-6=0,则2x=-6 |
在式子-
,
,x+y,
,
中,分式的个数有( )
| 3x |
| 2 |
| 4 |
| x-y |
| 1 |
| x |
| 5b |
| 3a |
| A、2个 | B、3个 | C、4个 | D、5个 |
 如图,BD⊥AC于点D,CE⊥AB于点E,BD、CE交于点E,BD、CE交于点F,AE=AD.求证:点F在∠A的平分线上.
如图,BD⊥AC于点D,CE⊥AB于点E,BD、CE交于点E,BD、CE交于点F,AE=AD.求证:点F在∠A的平分线上.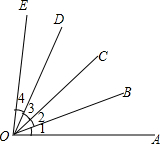 如图,已知∠1=20°,∠AOE=86°,OB平分∠AOC,OD平分∠COE
如图,已知∠1=20°,∠AOE=86°,OB平分∠AOC,OD平分∠COE