题目内容
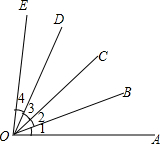 如图,已知∠1=20°,∠AOE=86°,OB平分∠AOC,OD平分∠COE
如图,已知∠1=20°,∠AOE=86°,OB平分∠AOC,OD平分∠COE(1)求∠3的度数;
(2)若以O为观察中心,OA为正东方向,则射线OD在什么方向﹖
(3)若以OA为钟表上的时针,OD为分针,且OA正好在“3”的下方不远,你知道此刻的时间吗(精确到分钟)﹖
考点:方向角,角的计算
专题:
分析:(1)根据角平分线的性质,可得∠AOC的度数,根据角的和差,可得∠COE,根据角平分线的性质,可得答案;
(2)根据角的和差,可得∠AOD的度数,根据方向角的表示方法,可得答案;
(3)根据时针旋转的度数减分针旋转的度数,可得答案.
(2)根据角的和差,可得∠AOD的度数,根据方向角的表示方法,可得答案;
(3)根据时针旋转的度数减分针旋转的度数,可得答案.
解答:解:如图 ,
,
(1)由OB平分∠AOC,∠1=20°,得∠AOC=40°,
由角的和差,得∠COE=∠AOE-∠AOC=86°-40°=46°,
由OD平分∠COE,得∠3=
∠COE=
×46°=23°;
(2)由角的和差,得∠AOD=∠AOE-∠EOD=86°-23°=63°,
射线OD在东偏北63°,即射线OD在北偏东27°;
(3)设3时x分,时针与分针相距63°,由时针旋转的角度减去分针旋转的角度,得
(3×30°+
x)-6x=63.
解得x=
,
答:此时的时间是3时
分.
 ,
,(1)由OB平分∠AOC,∠1=20°,得∠AOC=40°,
由角的和差,得∠COE=∠AOE-∠AOC=86°-40°=46°,
由OD平分∠COE,得∠3=
| 1 |
| 2 |
| 1 |
| 2 |
(2)由角的和差,得∠AOD=∠AOE-∠EOD=86°-23°=63°,
射线OD在东偏北63°,即射线OD在北偏东27°;
(3)设3时x分,时针与分针相距63°,由时针旋转的角度减去分针旋转的角度,得
(3×30°+
| 1 |
| 2 |
解得x=
| 54 |
| 11 |
答:此时的时间是3时
| 54 |
| 11 |
点评:本题考查了方向角,利用了角平分线的性质,角的和差,方向角的表示方法.

练习册系列答案
相关题目
下列二次根式中,不能与
合并的是( )
| 12 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、
|
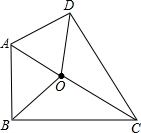 已知,如图,在四边形ABCD中,OA、OB、OC、OD分别是∠A、∠B、∠C、∠D的平分线,求证:AB+CD=AD+BC.
已知,如图,在四边形ABCD中,OA、OB、OC、OD分别是∠A、∠B、∠C、∠D的平分线,求证:AB+CD=AD+BC.