题目内容
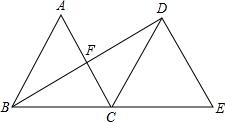 如图,△ABC是边长为2的等边三角形,将△ABC沿直线BC向右平移,使点B与点C重合,得到△DCE,连接BD,交AC于点F.
如图,△ABC是边长为2的等边三角形,将△ABC沿直线BC向右平移,使点B与点C重合,得到△DCE,连接BD,交AC于点F.(1)猜想AC与BD的位置关系,并证明你的结论;
(2)求线段BD的长.
考点:勾股定理,等边三角形的性质,平移的性质
专题:
分析:(1)由平移的性质可知BE=2BC=6,DE=AC=3,故可得出BD⊥DE,由∠E=∠ACB=60°可知AC∥DE,故可得出结论;
(2)在Rt△BDE中利用勾股定理即可得出BD的长.
(2)在Rt△BDE中利用勾股定理即可得出BD的长.
解答:解:(1)AC与BD的位置关系是:AC⊥BD.
∵△DCE由△ABC平移而成,
∴BE=2BC=4,DE=AC=2,∠E=∠ACB=60°,
∴DE=
BE,
∴BD⊥DE,
又∵∠E=∠ACB=60°,
∴AC∥DE,
∴BD⊥AC,
∵△ABC是等边三角形,
∴BF是边AC的中线,
∴BD⊥AC,BD与AC互相垂直平分;
(2)∵由(1)知,AC∥DE,BD⊥AC,
∴△BED是直角三角形,
∵BE=4,DE=2,
∴BD=
=2
.
∵△DCE由△ABC平移而成,
∴BE=2BC=4,DE=AC=2,∠E=∠ACB=60°,
∴DE=
| 1 |
| 2 |
∴BD⊥DE,
又∵∠E=∠ACB=60°,
∴AC∥DE,
∴BD⊥AC,
∵△ABC是等边三角形,
∴BF是边AC的中线,
∴BD⊥AC,BD与AC互相垂直平分;
(2)∵由(1)知,AC∥DE,BD⊥AC,
∴△BED是直角三角形,
∵BE=4,DE=2,
∴BD=
| BE2-DE2 |
| 3 |
点评:本题考查的是等边三角形的性质及平移的性质,熟知图形平移后的图形与原图形全等的性质是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在元旦前夕美化校园的活动中,七年级先安排31人去捡垃圾,18人去扫地,后又增派20人去支援他们,增援后捡垃圾的人数是扫地人数的2倍,求支援捡垃圾和扫地的人数分别有多少人,若设支援捡垃圾的有x人,则根据题意列出的方程是( )
| A、31+x=2×18 |
| B、31+x=2(38-x) |
| C、51-x=2(18+x) |
| D、51-x=2×18 |
在下列各方程中,无实数根的方程是( )
| A、x2-2x=1 | ||
B、x2-2
| ||
| C、x2-1=0 | ||
| D、x2-2x+3=0 |
 如图,正方形网格中每个小正方形边长都是1,每个小格的顶点叫格点,以格点为顶点的三角形叫做格点三角形.
如图,正方形网格中每个小正方形边长都是1,每个小格的顶点叫格点,以格点为顶点的三角形叫做格点三角形.