题目内容
如图，⊙O为△ABC的外接圆，∠A=72°，则∠BCO的度数为（ ）
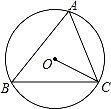
A．15° B．18° C．20° D．28°
B【考点】圆周角定理．
【专题】计算题．
【分析】连结OB，如图，先根据圆周角定理得到∠BOC=
2∠A=144°，然后根据等腰三角形的性质和三角形内角和定理计算∠BCO的度数．
【解答】解：连结OB，如图，∠BOC=2∠A=2×72°=144°，
∵OB=OC，
∴∠CBO=∠BCO，
∴∠BCO=
（180°﹣∠BOC）=×（180°﹣144°）=18°．
故选B．
【点评】本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．也考查了等腰三角形的性质．
练习册系列答案
阅读快车系列答案
相关题目
．如图1，△ABC的边BC在直线l上，AC⊥BC，且AC=BC；△EFP的边FP也在直线l上，边EF与边AC重合，且EF=FP．
（1）如图1，请你写出AB与AP所满足的数量关系和位置关系（不必证明）；
（2）将△EFP沿直线l向左平移到图2的位置时，EP交AC于点O，连接AP，BO．猜想并写出BO与AP所满足的数量关系和位置关系，并说明理由；
| |
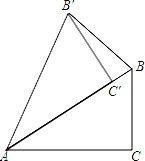
（3）将△EFP沿直线l继续向左平移到图3的位置时，EP的延长线交AC的延长线于点O，连接AP，BO．此时，BO与AP还具有（2）中的数量关系和位置关系吗？请说明
理由．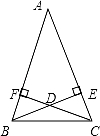 
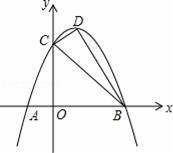
的图象与一次函数y=2x+1的图象的一个交点是（1，k），则反比例函数的解析式是 ．
米，则这个坡面的坡度为（ ）