题目内容
如图1,△ABC的边BC在直线l上,AC⊥BC,且AC=BC;△EFP的边FP也在直线l上,边EF与边AC重合,且EF=FP.
(1)如图1,请你写出AB与AP所满足的数量关系和位置关系(不必证明);
(2)将△EFP沿直线l向左平移到图2的位置时,EP交AC于点O,连接AP,BO.猜想并写出BO与AP所满足的数量关系和位置关系,并说明理由;

| |

 (3)将△EFP沿直线l继续向左平移到图3的位置时,EP的延长线交AC的延长线于点O,连接AP,BO.此时,BO与AP还具有(2)中的数量关系和位置关系吗?请说明
(3)将△EFP沿直线l继续向左平移到图3的位置时,EP的延长线交AC的延长线于点O,连接AP,BO.此时,BO与AP还具有(2)中的数量关系和位置关系吗?请说明 理由.
理由.
.解:(1)AB=AP;AB⊥AP.
(2)BO=AP;BO⊥AP.
证明:①由已知得:EF=FP,EF⊥FP,
∴∠EPF=45°.
又∵AC⊥BC,∴∠COP=∠CPO=45°.∴CO=CP.
在Rt△BCO和Rt△ACP中,BC=AC,∠BCO=∠ACP=90°,CO=CP,
∴Rt△BCO≌Rt△ACP.∴BO=AP.
②如图,延长BO交AP于点M.
∵Rt△BCO≌Rt△ACP,∴∠OBC=∠PAC.
在Rt△BCO中,∠OBC+∠BOC=90°,又∠BOC=∠AOM,
∴∠PAC+∠AOM=∠OBC+∠BOC=90°.∴∠OMA=90°.∴BO⊥AP.
成立.
证明:①如图,∵∠EPF=45°,∴∠CPO=45°.
又∵AC⊥BC,∴∠COP=∠CPO=45°.∴CO=CP.
在Rt△BCO和Rt△ACP中,
BC=AC,∠BCO=∠ACP=90°,CO=CP,
∴Rt△BCO≌Rt△ACP.∴BO=AP.
|

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
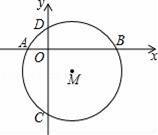
 ,AB=AC,BD平分∠ABC,∠A=36°,则∠1的度数为( )
,AB=AC,BD平分∠ABC,∠A=36°,则∠1的度数为( )


 B.
B.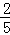 C.
C.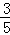 D.
D.