题目内容
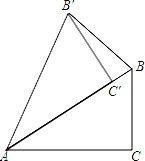
如图,把Rt△ABC绕点A逆 时针旋转40°,得到Rt△AB′C′,点C′恰好落在边AB上,连接BB′,则∠BB′C′= 度.
时针旋转40°,得到Rt△AB′C′,点C′恰好落在边AB上,连接BB′,则∠BB′C′= 度.
20 度.
【考点】旋转的性质.
【专题】计算题.
【分析】先根据旋转的性质得到∠ACB′=∠C=90°,∠BAB′=40°,AB=AB′,则利用等腰三角形的性质和三角形内角和定理可计算出∠ABB′=70°,然后利用互余计算∠BB′C′.
【解答】解:∵Rt△ABC绕点A逆时针旋转40°,得到Rt△AB′C′,点C′恰好落在边AB上,
∴∠ACB′=∠C=90°,∠BAB′=40°,AB=AB′,
∵AB=AB′,
∴∠ABB′=∠AB′B,
∴∠ABB′= (180°﹣40°)=70°,
(180°﹣40°)=70°,
∴∠BB′C′=90°﹣∠CBB′=20°.
故答案为20.
【点评】本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
 是AC的中点.若AD=6,DE=5,则CD的长等于 .
是AC的中点.若AD=6,DE=5,则CD的长等于 .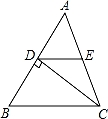
 a3 C. (a2)3=a6 D. 2a+3a2=5a3
a3 C. (a2)3=a6 D. 2a+3a2=5a3 
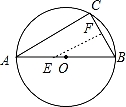

 的中点,∠ABC=50°,则∠DAB等于( )
的中点,∠ABC=50°,则∠DAB等于( )
