题目内容
在一只不透明的布袋中装有红球、黄球各若干个,这些球除颜色外都相同,充分摇匀.
(1)若布袋中有3个红球,1个黄球.从布袋中一次摸出2个球,计算“摸出的球恰是一红一黄”的概率(用“画树状图”或“列表”的方法写出计算过程);
(2)若布袋中有3个红球,x个黄球.
请写出一个x的值 ,使得事件“从布袋中一次摸出4个球,都是黄球”是不可能的事件;
(3)若布袋中有3个红球,4个黄球.
我们知道:“从袋中一次摸出4个球,至少有一个黄球”为必然事件.
请你仿照这个表述,设计一个必然事件: .
(1)若布袋中有3个红球,1个黄球.从布袋中一次摸出2个球,计算“摸出的球恰是一红一黄”的概率(用“画树状图”或“列表”的方法写出计算过程);
(2)若布袋中有3个红球,x个黄球.
请写出一个x的值
(3)若布袋中有3个红球,4个黄球.
我们知道:“从袋中一次摸出4个球,至少有一个黄球”为必然事件.
请你仿照这个表述,设计一个必然事件:
考点:列表法与树状图法,随机事件
专题:开放型
分析:(1)依据题意先用列表法或画树状图法分析所有可能,即可得出答案;
(2)根据不可能事件的概率为0,填空即可;
(3)根据必然事件的概率为:1,填空即可.
(2)根据不可能事件的概率为0,填空即可;
(3)根据必然事件的概率为:1,填空即可.
解答:解:(1)设三个红球分别是1、2、3,黄球为4,列表得:
(1,2),(1,3),(1,4),(2,1),(2,3),(2,4),(3,1),(3,2),(3,4),(4,1),(4,2),(4,3)共12种; 所以摸出的球恰是一红一黄”的概率=
=
;
(2)因为不可能事件的概率为0,所以x可取1≤x≤3之间的整数,
故答案为:1或2或3;
(3)因为必然事件的概率为1,所以从袋中一次摸出5个球,至少有两个黄球是必然事件,
故答案为:从袋中一次摸出5个球,至少有两个黄球.
y x (x,y) | 1 | 2 | 3 | 4 |
| 1 | (1,2) | (1,3) | (1,4) | |
| 2 | (2,1) | (2,3) | (2,4) | |
| 3 | (3,1) | (3,2) | (3,4) | |
| 4 | (4,1) | (4,2) | (4,3) |
| 6 |
| 12 |
| 1 |
| 2 |
(2)因为不可能事件的概率为0,所以x可取1≤x≤3之间的整数,
故答案为:1或2或3;
(3)因为必然事件的概率为1,所以从袋中一次摸出5个球,至少有两个黄球是必然事件,
故答案为:从袋中一次摸出5个球,至少有两个黄球.
点评:此题主要考查了列表法求概率,列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
计算(-2xy)2÷xy2,正确的结果是( )
| A、2x | B、4x | C、2 | D、4 |
 如图,?ABCD中,∠B=70°,点E是BC的中点,点F在AB上,且BF=BE,过点F作FG⊥CD于点G,则∠EGC的度数为( )
如图,?ABCD中,∠B=70°,点E是BC的中点,点F在AB上,且BF=BE,过点F作FG⊥CD于点G,则∠EGC的度数为( )| A、35° | B、45° |
| C、30° | D、55° |
若一个三角形三个内角度数的比为2:3:1,那么这个三角形是( )
| A、直角三角形 |
| B、钝角三角形 |
| C、锐角三角形 |
| D、等边三角形 |
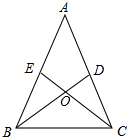 已知:如图,在锐角三角形ABC中,AB=AC,两条高BD与CE相交于点O,求证:OB=OC.
已知:如图,在锐角三角形ABC中,AB=AC,两条高BD与CE相交于点O,求证:OB=OC.